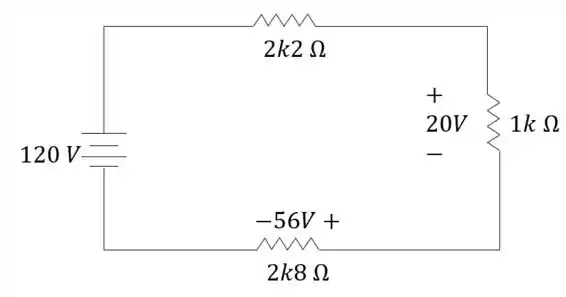
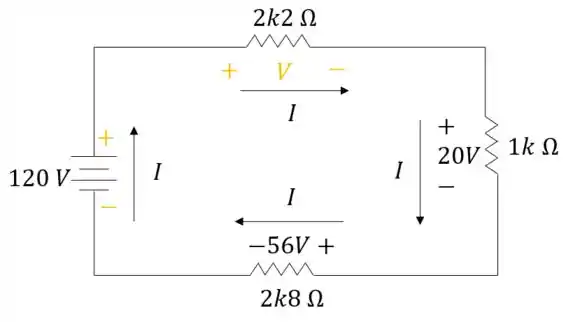
Em uma Usina Hidrelétrica situada no Rio Iguaçu, o sistema de controle é em corrente contínua, cujo circuito equivalente está representado na figura abaixo. Em cima destas informações, quais são os valores da corrente no resistor de ?
Passo 1
Bora para mais uma questãozinha!!!
Olhando o circuito, vemos que tem umas resistências meio esquisitas, não é? O que será que significa aquele e aquele ? Será que foi erro de digitação? Não! Essa é uma outra forma de escrever e . Nessa notação o é escrito na posição onde ficaria a vírgula!
Show! Agora descobrimos que tem nada de errado no enunciado, podemos continuar a questão 😊
Como sabemos as tensões de toda a malha exceto da queda de tensão sob o resistor de , podemos aplicar a Lei de Kirchhoff nesta malha!
Primeiro passo é estabelecer a corrente:
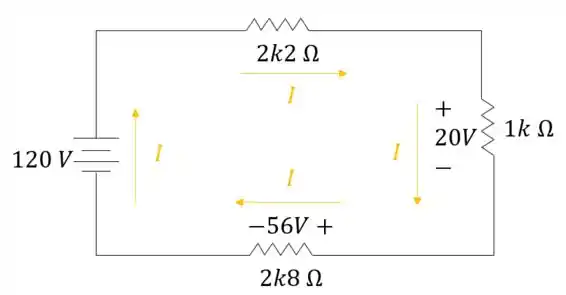
O motivo de ter colocado nesse sentido é que como sabemos que em resistores, a corrente entra pelo polo positivo e sai pelo polo negativo, essa foi a primeira condição que atendemos já que o enunciado nos deu as polaridades dos resistores.
Passo 2
Evidenciar a polaridade dos outros elementos.
Vou colocar um exemplo aqui pra gente lembrar das regrinhas, beleza?
- Quando a corrente passa pelo resistor, ela entra pelo polo positivo e sai pelo polo negativo da queda de tensão:
- A fonte de tensão já vem definido o polo positivo e o polo negativo de acordo com seu símbolo:
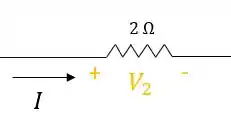
Essa queda de tensão no resistor será igual a:
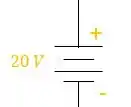
Vamos definir todos os polos positivos e negativos para o circuito:
Passo 3
Vamos aplicar a Lei de Kirchhoff nessa malha?
Percorrendo de acordo com a circulação da corrente :
- Fonte de tensão com sinal positivo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
Pela Lei de Kirchhoff, a soma de todas as tensões e quedas em uma mesma malha deve ser igual a zero!
Isolando a incógnita que desejamos descobrir de um lado só, podemos passar para o outro lado da igualdade e ela se tornará positiva:
Realizando essas subtrações:
Encontramos a queda de tensão sobre o resistor ! Mas como vamos encontrar a corrente?
Passo 4
Vamos olhar de novo para o resistor:
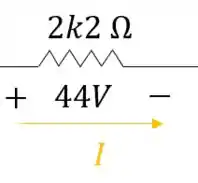
Sabemos a queda de tensão e a resistência :
Agora não caímos mais na pegadinha da notação, né haha. Mas o que significa ? Significa que estamos multiplicando aquela quantidade por :
Como não sabemos a corrente , podemos utilizar a Lei de Ohm, veja:
Aplicando os valores que conhecemos:
Isolando o , teremos:
Realizando essa conta chegamos ao valor de: