Calcule , e :
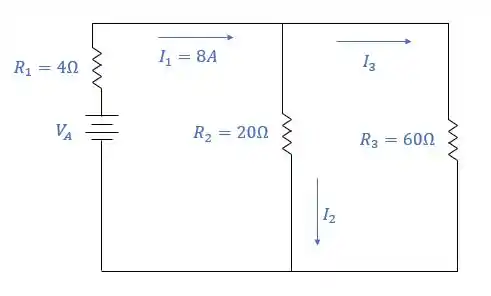
Passo 1
Vamos pensar o seguinte, como os resistores e estão em paralelo, eles devem ter a mesma queda de tensão entre os seus terminais, correto? Veja:
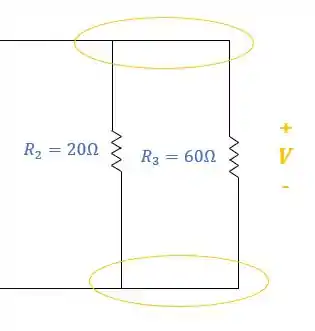
Mas quanto vale essa queda de tensão? Isso depende da corrente que passa em cada resistor:
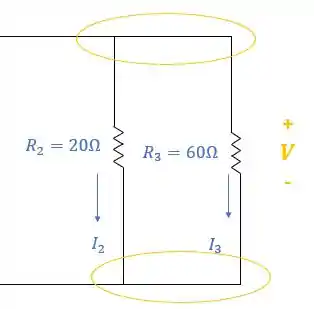
Lembrando da fórmula da primeira lei de Ohm
temos que
Como já concluímos que , então podemos escrever
Ou seja, achamos uma relação entre e :
Substituindo os valores dos resistores:
Isolando o de um lado da igualdade, temos que passar o número que o multiplica para o outro lado dividindo:
Que será igual a:
Passo 2
Lembra da Lei de Kirchhoff para correntes? A soma de todas as correntes que entram em um nó é igual a soma de todas as correntes que saem do nó:
Quem é o nosso nó? Esse aqui:
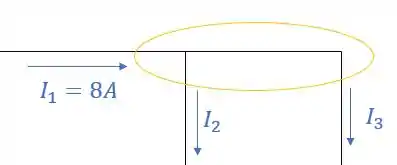
Quem são as correntes que entram? Apenas que vale
Enquanto as correntes que saem do nó são e :
Achamos mais uma relação entre e não é? Agora temos o sistema:
Substituindo a primeira equação na segunda, temos:
Somando a , temos:
Agora para encontrar basta passar o que está multiplicando para o outro lado dividindo
Então encontramos :
Como , logo:
Isolando a corrente de um lado da equação:
Chegamos na segunda corrente!
Apenas utilizando Lei de Kirchhoff e nossos conhecimentos sobre Lei de Ohm!
Passo 3
Agora queremos encontrar a tensão da fonte , mas como? Primeiro vamos olhar para a primeira malha:
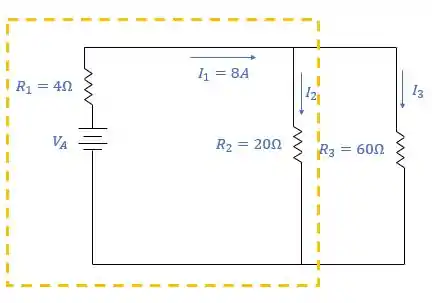
Sabemos todas as correntes e todos os resistores, então vamos aplicar Lei de Kirchhoff das malhas para essa malha destacada, certo? Vem comigo!
O primeiro passo é marcar o sentido da corrente que iremos acompanhar, nesse caso, vou usar o sentido anti-horário, pois as correntes e já circulam nesse sentido:
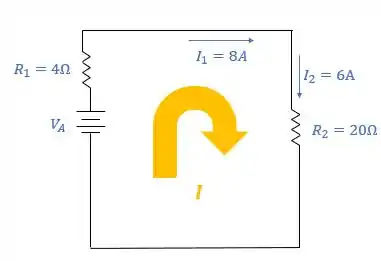
Passo 4
Agora vamos marcar os polos positivos e negativos, além de calcular as quedas de tensão nos resistores. Temos algumas regrinhas bem simples:
- Quando a corrente passa pelo resistor, ela entra pelo polo positivo e sai pelo polo negativo da queda de tensão:
- A fonte de tensão já define o polo positivo e o polo negativo de acordo com seu símbolo, o traço maior sempre será o positivo e o menor sempre será o negativo:
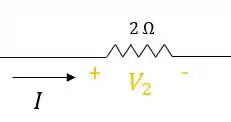
Essa queda de tensão no resistor obedece a primeira lei de Ohm
Então, será igual a:
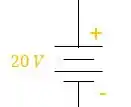
Vamos definir todos os polos positivos e negativos para o circuito:
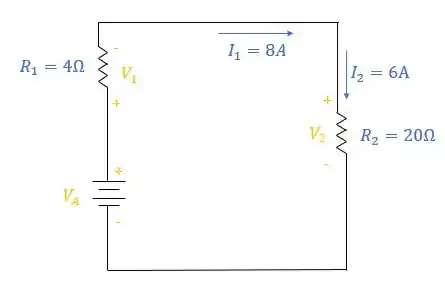
Passo 5
Vamos calcular as quedas de tensão nos resistores. Como a resistência está ligada em série com a fonte, por ela circula a corrente , então:
Substituindo os valores que o circuito nos fornece:
Agora pelo resistor circula a corrente , logo a queda de tensão será:
Substituindo os valores que o circuito nos fornece:
Passo 6
Agora que sabemos as quedas de tensão em cada resistor, vamos agora percorrer essa malha como se fôssemos a corrente. Por onde a corrente entrar pelo polo positivo e sair pelo negativo, iremos subtrair o valor. Enquanto por onde a corrente entrar pelo polo negativo e sair pelo polo positivo, iremos somar.
Calma, vamos ver cada um dos elementos.
- Começando pela primeira fonte de tensão de :
- O primeiro resistor tem uma queda de tensão igual a :
- O segundo resistor tem uma queda de tensão igual a :
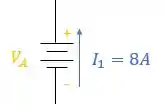
Como a corrente entra pelo polo negativo e sai pelo polo positivo, vamos assumir como valor positivo:
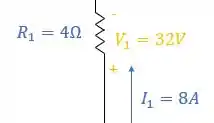
Como a corrente entra pelo polo positivo e sai pelo polo negativo, vamos assumir como valor negativo:

Como a corrente entra pelo polo positivo e sai pelo polo negativo, vamos assumir como valor negativo:
Vamos finalmente montar a nossa Lei de Kirchhoff que diz que a soma de todas as tensões de uma malha deve ser igual a zero. Veja:
Resolvendo essa continha
Isolando o , encontramos
Chegamos na resposta final!