Um circuito em série é composto por uma fonte de tensão contínua de , um resistor de , cuja queda de tensão tem valor desconhecido e um resistor de valor desconhecido, cuja queda de tensão é de . Por este circuito circula a corrente de valor . Para melhor visualização o circuito é apresentado abaixo. Os valores de , e no circuito mencionado são:
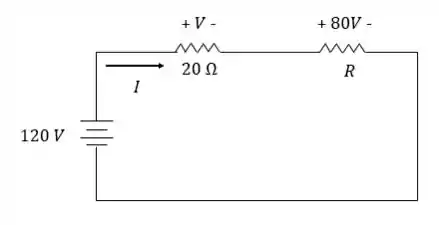
Passo 1
Vamos começar relembrando o que a Lei de Kirchhoff para tensões nos diz:
A soma das tensões de uma malha deve ser igual a zero
Mas temos que ver que em um circuito temos fontes de tensão e quedas de tensão.
Vamos primeiro evidenciar os polos positivo e negativo de cada elemento:
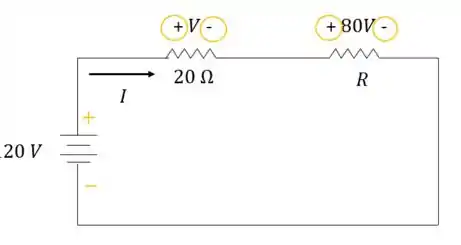
Passo 2
Por onde a corrente entrar pelo polo positivo e sair pelo negativo, iremos subtrair o valor. Enquanto por onde a corrente entrar pelo polo negativo e sair pelo polo positivo, iremos somar.
Calma, vamos ver cada um dos elementos.
- A fonte de tensão
- A queda de tensão no resistor de
- A queda de tensão no resistor
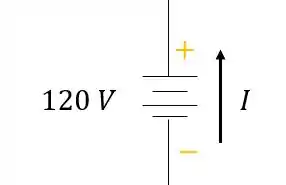
Será positiva:
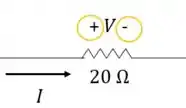
Será negativa:
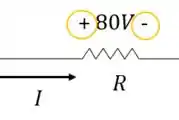
Será negativa:
Passo 3
Vamos agora montar a nossa equação de malha:
Podemos passar a queda de tensão , que desejamos descobrir, para o outro lado:
Pronto, sabemos que a queda de tensão no resistor de é igual a !
Passo 4
Sabe como vamos encontrar a corrente? Através da Lei de Ohm:
Olhe nossos valores:
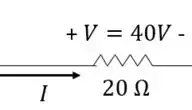
Logo:
Aplicando na equação da Lei de Ohm:
Passando o para o outro lado da equação, ficamos com
Achamos a corrente!!!
Passo 5
Agora vamos olhar para o resistor
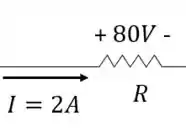
Pela Lei de Ohm:
Podemos substituir os valores:
Vamos descobrir o valor do resistor :
Isolando o resistor de um lado da equação:
Pronto, encontramos todos os valores!
Resposta
d)