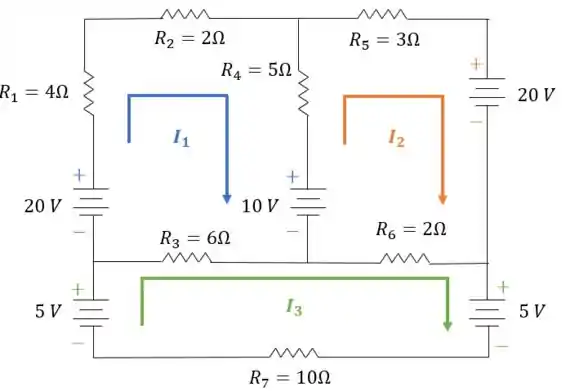
Equacione o circuito abaixo, usando as leis de Kirchhoff:
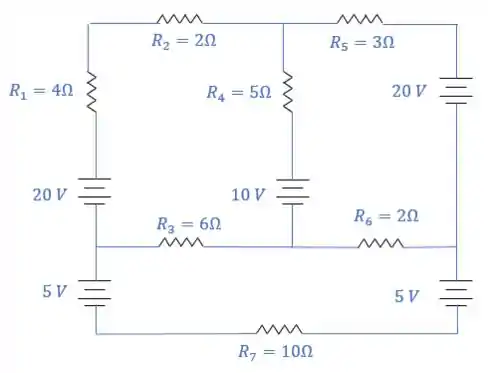
Passo 1
Aeeee última questão para fechar com chave de ouro!!!
Olha só o que enunciado nos pediu, para equacionar. Então vai ser isso que faremos, não iremos resolver, apenas equacionar, ta bom? Então vamos lá!
O primeiro passo é definirmos nossas correntes, então como temos malhas, teremos três correntes, veja:
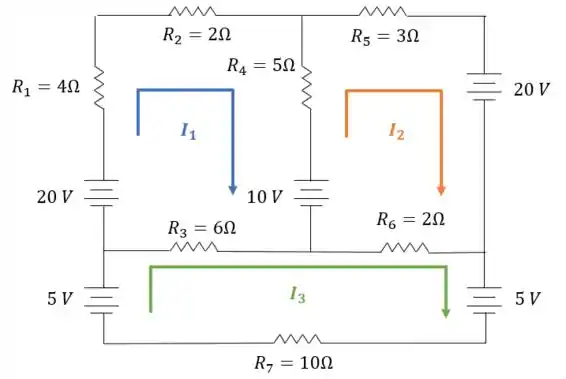
O sentido das correntes foi escolhido arbitrariamente, você poderia escolher outros sentidos, se preferisse. Mas minha dica é escolher no mesmo sentido para evitar confusão no futuro 😉
Passo 2
Já somos capazes de estabelecer os polos positivo e negativo de cada queda de tensão, certo?
Vou mostrar um exemplo só para lembrarmos da regrinha, beleza?
- Quando a corrente passa pelo resistor, ela entra pelo polo positivo e sai pelo polo negativo da queda de tensão:
- A fonte de tensão já vem definido o polo positivo e o polo negativo de acordo com seu símbolo:
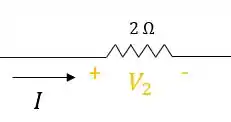
Essa queda de tensão no resistor será igual a:
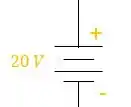
Vamos definir todos os polos positivos e negativos para o circuito. Primeiro para as fontes de tensão:
Agora os polos positivo e negativo para as malhas , e :
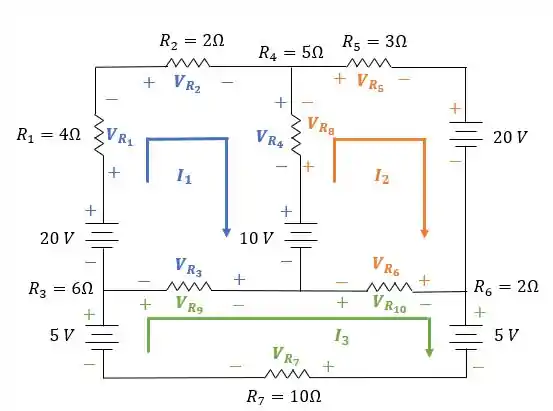
Passo 3
Vamos calcular as quedas de tensão nos resistores. Utilizaremos a Lei de Ohm:
- Calculando :
- Calculando :
- Calculando :
- Calculando :
- Calculando :
- Calculando :
- Calculando :
- Calculando :
- Calculando :
- Calculando :
Fazemos essa subtração, pois quem causa esse posicionamento dos polos positivo e negativo de é a corrente , porém a corrente é contrária a essa queda de tensão.
Estamos fazendo a mesma subtração, só que invertemos as correntes por conta da polaridade!
Passo 4
Vamos aplicar a Lei de Kirchhoff nessas malhas? Vamos olhar de novo para a primeira malha:
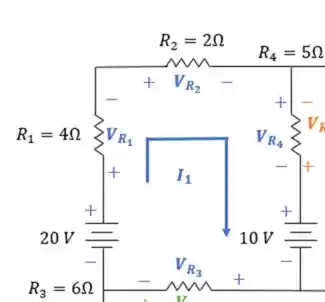
Percorrendo de acordo com a circulação da corrente :
- Fonte de tensão com sinal positivo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Fonte de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Fonte de tensão com sinal positivo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Fonte de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Fonte de tensão com sinal positivo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Fonte de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
Montando a equação para essa malha, temos:
Pela Lei de Kirchhoff, a soma de todas as tensões e quedas em uma mesma malha deve ser igual a zero!
Vamos substituir as quedas de tensão calculadas anteriormente
Aplicando a distributiva em:
E em:
Lembrando que multiplicação entre um número positivo com um número negativo é igual a um número negativo. Porém a multiplicação entre dois números negativos é iguala um número positivo:
E
Então voltamos para a equação da primeira malha:
Vamos somar todos os termos que são multiplicados por :
Podemos subtrair esse com o
Achamos a primeira relação, vamos guardar ela com carinho! Enquanto isso vamos olhar para a segunda malha!
Passo 5
Olhando agora para a segunda malha:
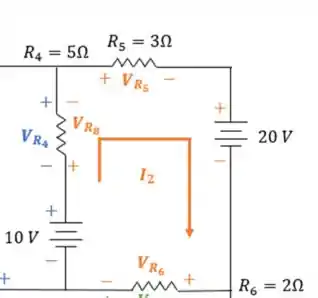
Percorrendo de acordo com a circulação da corrente :
Montando a equação para essa malha, temos:
Pela Lei de Kirchhoff, a soma de todas as tensões e quedas em uma mesma malha deve ser igual a zero!
Vamos substituir as quedas de tensões que encontramos anteriormente
Aplicando a distributiva em:
E em:
Lembrando que multiplicação entre um número positivo com um número negativo é igual a um número negativo. Porém a multiplicação entre dois números negativos é iguala um número positivo:
E
Então voltamos para a equação da segunda malha:
Vamos somar todos os termos que são multiplicados por :
Podemos subtrair o com o
Achamos a segunda relação, vamos guardar mais ela com carinho! Enquanto isso vamos olhar para a terceira e última malha!
Passo 6
Olhando a terceira e última malha:
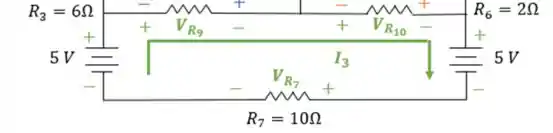
Percorrendo de acordo com a circulação da corrente :
Pela Lei de Kirchhoff, a soma de todas as tensões e quedas em uma mesma malha deve ser igual a zero!
Vamos substituir as quedas de tensão encontradas acima
Aplicando a distributiva em:
E em:
Lembrando que multiplicação entre um número positivo com um número negativo é igual a um número negativo. Porém a multiplicação entre dois números negativos é iguala um número positivo:
E
Então voltamos para a equação da terceira malha:
Vamos somar todos os termos que são multiplicados por :
Podemos subtrair o com o outro
Achamos a terceira relação! Cumprimos o nosso propósito! Vamos relembrar todas as equações? Elas são: