Exercícios Resolvidos de Limites de Confiança

Exercício 2 1 3 4 5

Enunciado

Considerando um grande número de medidas de forma que s seja uma boa estimativa de , determine que nível de confiança foi usado para cada um dos intervalos de confiança:

Passo 1

Opaa, temos então várias expressões para intervalos de confiança!

Só pra refrescar a memória, vamos ver a expressão geral, o problema diz que é uma boa estimativa de , então podemos considerar:

E como a gente pode saber o nível de confiança?!

Muito simples, a gente vai consultar essa tabelinha aqui:

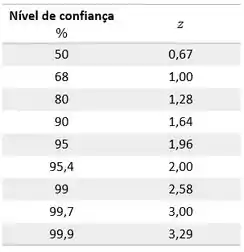
E como podemos ver, o é o número que esta multiplicando o em cada letra! Então vamos começar com a letra

Consultando a tabela achamos que para o nível de confiança é de !

Passo 2

Agora vamos fazer a mesma coisa para as outras letras!

Na letra temos , consultando a tabela ;

Para , essa é a nossa letra ;

E pra acabar, para , ;

Molezinha, não é!?

Resposta

Exercícios de Livros Relacionados

Problema Desafiador. Os dados que seguem representam três conjuntos de dados para a massa atômica do antimônio obtidos a partir do trabalho de Willard e McAlpine:(e) Compare as médias de todos os três

Descreva com suas próprias palavras por que o intervalo de confiança em relação à média de cinco medidas é menor que aquele para um único resultado.

Discuta como a dimensão do intervalo de confiança da média é influenciada pelos seguintes aspectos (todos os outros fatores são constantes):(a) O tamanho N da amostra.(b) O nível de confiança.(c) O de

No Problema 7-17, a medida realizada na terceira semana é suspeita de ser um valor anômalo. Utilize o teste Q para determinar se o valor pode ser rejeitado em um nível de confiança de 95%.

Um método baseado em absorção atômica, desenvolvido para a determinação de cobre em combustíveis, gerou um desvio padrão combinado scomb 0,32 mg de Cu/Ml (s S s). A análise do óleo do motor de uma aer