Cada uma das quatro rodas do veículo tem uma massa de e está montada em um eixo de de diâmetro. A massa total do veículo é , incluindo as rodas, e está distribuída igualmente pelas quatro rodas. Se uma força é necessária para manter o veículo rodando sob uma velocidade constante baixa sobre uma superfície horizontal, calcule o coeficiente de atrito que existe nos mancais das rodas. (Sugestão: Desenhe um diagrama de corpo livre completo para uma roda.)
Passo 1
Como foi sugerido, vamos montar o nosso diagrama de corpo livre para uma das rodas:
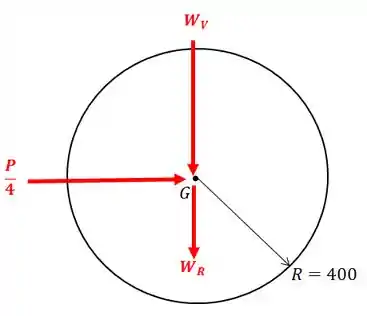
O peso do veículo () suportado por cada roda vai ser o peso total dividido entre as quatro rodas. Mas repare que a massa de também inclui a massa das quatro rodas.
Então, a massa do veículo () vai ser:
Com isso, o peso do veículo fica:
E o peso de cada roda () será:
Repare também a força foi dividida entre as quatro rodas e por isso ficamos com:
Beleza?
Passo 2
Fazendo o equilíbrio de forças verticais na roda, surge uma força normal igual a:
E fazendo o equilíbrio das forças horizontais, temos:
Então, vamos ter o seguinte diagrama de corpo livre:
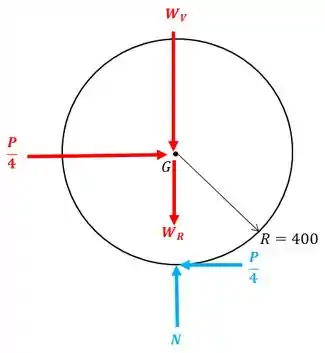
Repare que se fizermos o somatório de momentos com relação ao ponto , surge um momento devido a força .
Então, para termos um equilíbrio precisa surgir um momento :
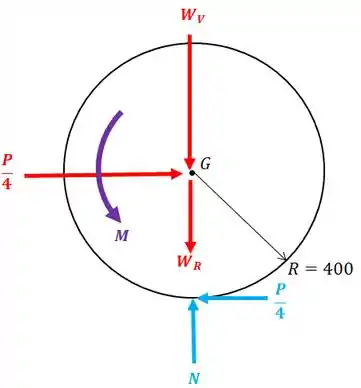
Passo 3
Sabendo que o momento em um mancal é calculado por:
Onde, é a carga suportada pelo mancal que vai ser o peso do veículo:
E é o raio do mancal que vale:
Então, vamos ter que:
Agora sim podemos calcular o coeficiente de atrito: