Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mancais

Ver Teoria
Exercício 21345678

Enunciado

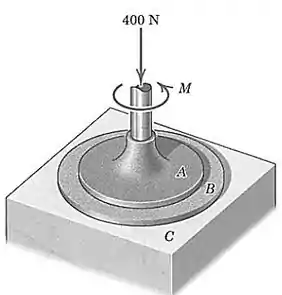
O disco circular A é colocado sobre o topo do disco B e submetido a uma força compressiva de 400   N . Os diâmetros de A   e   B valem 225   m m   e   300   m m , respectivamente, e a pressão em cada disco é constante em toda a superfície. Se o coeficiente de atrito entre A e B vale 0,4 , determine o momento M que fará com que A deslize sobre B . Além disso, qual é o coeficiente de atrito μ mínimo entre B e a superfície de apoio C que impedirá que B gire?

Passo 1

Para calcular o momento temos que usar a nossa fórmula aqui:

M = 2 3 μ P R

Onde R é o raio do círculo menor, pois o disco A é que vai girar. E P é a força compressiva de 400   N .

Passo 2

Para o primeiro caso, estamos considerando o momento que fará com que A deslize sobre B . Basicamente, estaremos calculando o momento máximo que causa a iminência do movimento.

Sendo assim, o raio R que vamos usar é o raio do círculo menor:

R A = D A 2 = 112,5   m m

Então, o momento será:

M = 2 3 μ P R A     →       M = 2 3 0,4 400 0,1125

∴

M = 12   N ⋅ m

Passo 3

Agora queremos saber qual o coeficiente de atrito mínimo que impede o giro da placa B sobre C .

O que continua constante nos dois casos? O momento!!!

Como um momento de 12   N ⋅ m está sendo aplicado na placa B , a placa C precisará aplicar um momento contrário, mas de mesmo módulo, para impedir a rotação. Sendo assim:

M ' = 12   N ⋅ m

Ah, e agora o raio será o raio de B :

R B = D B 2 = 150   m m = 0,15   m

Então, o momento será calculado pela nossa fórmula:

M ' = 2 3 μ m í n P R B

∴

12 = 2 3 μ m í n 400 0,15     →       μ m í n = 3 ( 1 2 ) 2 400 0,15

∴

μ m í n = 0,3

Resposta

M = 12   N ⋅ m

μ m í n = 0,3

Exercícios de Livros Relacionados

O disco de embreagem é usado nas transmissões de automóveis padrão. Se quatro molas são usadas para manter os dois discos A e B juntas, determine a força em cada mola necessária para transmitir um mom
Se a mola exerce uma força de 4500N sobre o bloco determine o torque M necessário para girar o eixo. O coeficiente de atrito estático em todas as superfícies de contato é μ s = 0,3 .
135- Calcule o momento M aplicado ao cilindro inferior do par, ambos com 20k g , que permitirá que eles rolem para baixo lentamente. Os coeficientes de atrito estático e dinâmico para todas as superfí
A roldana dupla mostrada na figura é fixada a um eixo de 10m m de raio que se ajusta com folga a um mancal fixo. Sabendo que o coeficiente de atrito estático entre o eixo e o mancal pouco lubrificado
Uma alavanca de peso desprezível está encaixada com folga em um eixo de 75m m de diâmetro. Observa-se que a alavanca apenas inicia um movimento de rotação se a massa de 3k g é adicionada em C . Determ