Calcule o torque necessário para girar o carretel de cabo telefônico de no sentido horário contra a força trativa de no cabo. O diâmetro do mancal vale e o coeficiente de atrito para o mancal é
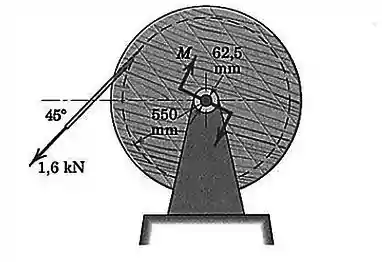
Passo 1
Vamos lembrar um conceito que vimos em tópicos anteriores: o conceito de sistema força binário resultante.
Queremos calcular o momento necessário para fazer o carretel girar no sentido horário, certo? Mas antes disso, temos que calcular os momentos contrários a esse movimento.
O momento da força de em relação ao ponto no centro do carretel é dado por:
Isso no sentido anti-horário.
Passo 2
Agora vamos representar o sistema de forças completo:
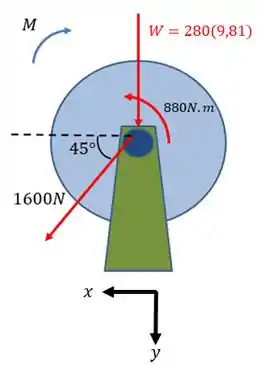
A força peso do carretel tem módulo de:
Tá vendo? Deslocamos a força de para o ponto que queremos, além de representar o seu momento por meio de um binário. Que ponto é esse? É o ponto localizado a uma distância do centro do sistema.
Agora devemos calcular a força resultante devido à força aplicada e ao peso.
Assim:
Assim, o módulo dessa força vale:
Passo 3
Agora vamos descobrir o ângulo de atrito:
Com isso vamos poder calcular . É importante calcular porque a força resultante vai estar localizada a essa distância do centro do círculo. Repare que no enunciado foi dado o diâmetro do mancal que vale , mas temos que usar o raio do mancal para calcular :
Com isso, podemos calcular o momento gerado pela força resultante:
Passo 4
Show de bola! Já temos tudo que precisamos para calcular o momento . Esse momento tem que se opor aos dois momentos que calculamos antes de forma a fazer com que o sistema fique na iminência de girar. Assim: