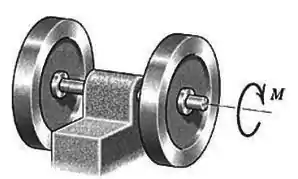
Os dois rotores estão montados no mesmo eixo, que está apoiado por um mancal radial entre eles. Cada rotor tem uma massa de e o diâmetro do eixo vale Se um momento de é necessário para manter a rotação dos rotores e do eixo em uma velocidade constante baixa, calcule:
- O coeficiente de atrito no mancal.
- O raio do círculo de atrito.
Passo 1
No caso de um mancal radial, podemos relacionar a carga radial , o raio do eixo , o seno do ângulo de atrito () e o momento com a seguinte fórmula:
Quem é a carga radial nesse caso? É o próprio peso dos rotores!
Então, vamos calcular este peso:
Multiplicamos o peso por , pois temos rotores!
Passo 2
O raio do eixo vale:
Agora podemos calcular o ângulo de atrito sabendo que o momento necessário para manter a rotação dos rotores e do eixo é de , então:
Assim, o ângulo de atrito será:
Sabendo o ângulo de atrito podemos calcular o coeficiente de atrito , pois:
Então, podemos calcular da seguinte forma:
Passo 3
E para calcular o raio do círculo de atrito? Basta a gente usar: