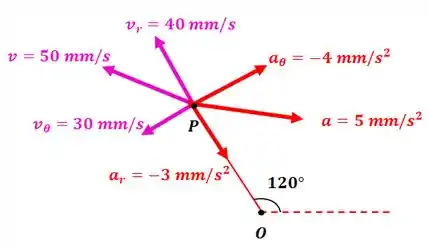
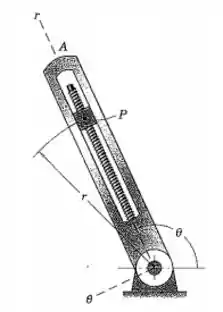
O movimento do bloco deslizando na ranhura radial rotativa é controlado pelo parafuso como mostrado. Para o instante representado , e . Além disso, o parafuso gira a uma velocidade constante fornecendo . Para este instante, determine os módulos da velocidade e da aceleração de . Desenhe e a para .
Passo 1
Temos:
E:
Então:
Passo 2
E:
E:
Assim:
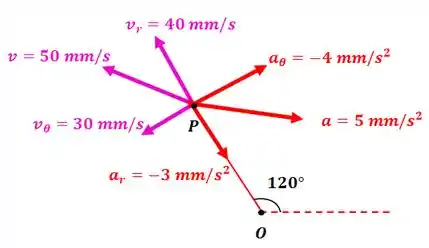
Resposta