Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Coordenadas Polares, Tangenciais e Normais

Ver Teoria
Exercício 2134567

Enunciado

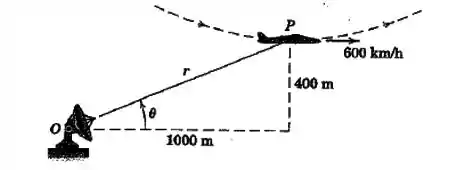
Na parte inferior de uma acrobacia aérea na qual o avião descreve um círculo em um plano vertical ( r θ ) a uma altitude de 400 metros, o avião P tem uma velocidade horizontal de 600   k m / h e nenhuma aceleração horizontal. O raio de curvatura da trajetória é 1200   m . Para o radar de rastreamento em O , determine os valores de r ¨ e θ ¨ registrado para esse instante.

Passo 1

Vamos primeiro desenhar esse sistema mostrando os ângulos de interesse:

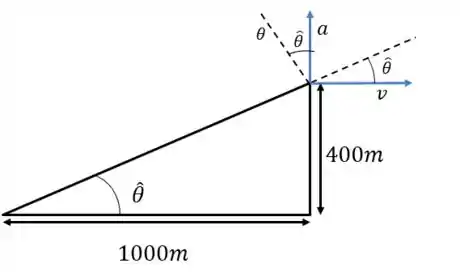
Quem é a aceleração a ? É a aceleração centrípeta do avião, já que ele está descrevendo uma curva. E v é a velocidade do próprio avião.

Quanto vale θ ^ ?

θ ^ = a r c t g 400 1000 = a r c t g 0,4 = 21,8 °

E r :

r = 1000 2 + 400 2 = 1077   m

Passo 2

Bom, a velocidade nós temos que passar para m / s :

v = 600   k m / h = 600 3,6 = 166,7   m / s

Com isso, podemos calcular a aceleração centrípeta:

a = a c t p = v 2 R = 166,7 2 1200 = 23,1   m / s 2

Vamos calcular primeiro v r :

v r = r ˙

Já que é a taxa de crescimento ou decrescimento do raio r . Vamos ter que decompor v na direção r :

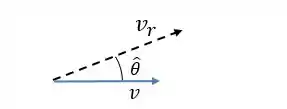
Assim:

v r = v c o s 21,8 ° = 166,7 cos ⁡ 21,8 ° = 154,7   m / s

E v θ ? v θ é a velocidade na direção θ :

v θ = - 166,7 s e n 21,8 ° = - 61,9   m / s

Só que:

v θ = r θ ˙     →       - 61,9 = 1077 θ ˙

∴

θ ˙ = - 0,0575 r a d / s

Passo 3

E a aceleração radial? Da mesma forma que a velocidade radial, podemos usar seno e cosseno para calcular:

a r = a s e n 21,8 ° = 23,1 s e n 21,8 ° = 8,58   m / s 2

Só que:

a r = r ¨ - r θ ˙ 2

Então:

8,58 = r ¨ - 1077 - 0,0575 2

∴

r ¨ = 12,15 m / s 2

Passo 4

E a aceleração na direção θ ? Será:

a θ = acos ⁡ 21,8 ° = 23,1 cos ⁡ 21,8 ° = 21,45   m / s 2

Lembrando que:

a θ = r θ ¨ + 2 r ˙ θ ˙

Assim:

21,4 = 1077 θ ¨ + 2 . 154,7 - 0,0575 → θ ¨ = 0,0365   r a d / s 2

Resposta

r ¨ = 12,15   m / s 2

θ ¨ = 0,0365   r a d / s 2

Exercícios de Livros Relacionados

Quando o carro chega ao ponto A, ele tem velocidade escalar de 25m / s . Se os freios são acionados, sua velocidade escalar é reduzida em a t = - 1 4 t 1 2m / s 2 . Determine a intensidade da aceleraç
Um carro move-se ao longo de uma curva circular de raio r = 90 m. No instante mostrado, a sua taxa angular de rotação é θ ˙ = 0,4r a d / s , a qual está aumentando a uma taxa de θ ¨ = 0,2r a d / s 2 .
Se o carrinho da montanha-russa parte do repouso em A e sua velocidade escalar aumenta em a t = 6 - 0,06 sm / s 2 , determine a intensidade da sua aceleração quando ela alcança B onde s B = 40m .
O carro está viajando a uma velocidade escalar de 30m / s . O motorista aciona os freios em A e, assim, reduz a velocidade escalar do carro a uma razão de a t = - t / 8m / s 2 , onde t é dado em s . D
2/115) Na parte inferior A da acrobacia aérea na qual o avião descreve um círculo em um plano vertical , o módulo da aceleração total do avião é de 3 g . Se a velocidade do avião em relação ao ar é de