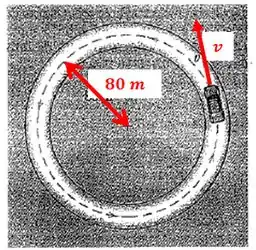
Um carro de teste parte do repouso em uma pista horizontal circular de de raio e aumenta sua velocidade a uma taxa uniforma para atingir os em segundos. Determine o módulo da aceleração total do carro segundos após a partida.
Passo 1
Vamos primeiro calcular a aceleração média do carro. Podemos fazer isso da seguinte forma:
Perceba que a velocidade está em Vamos dividir por para passar para :
Assim:
Assim, a velocidade tangencial em função do tempo pode ser dada por:
Passo 2
Beleza, então a velocidade para o tempo
Assim, podemos calcular a aceleração centrípeta:
Passo 3
Assim, a aceleração total é dada por:
Resposta
Exercícios de Livros Relacionados
Quando o carro chega ao ponto A, ele tem velocidade escalar de 25m / s . Se os freios são acionados, sua velocidade escalar é reduzida em a t = - 1 4 t 1 2m / s 2 . Determine a intensidade da aceleraç
Um carro move-se ao longo de uma curva circular de raio r = 90 m. No instante mostrado, a sua taxa angular de rotação é θ ˙ = 0,4r a d / s , a qual está aumentando a uma taxa de θ ¨ = 0,2r a d / s 2 .
Se o carrinho da montanha-russa parte do repouso em A e sua velocidade escalar aumenta em a t = 6 - 0,06 sm / s 2 , determine a intensidade da sua aceleração quando ela alcança B onde s B = 40m .
O carro está viajando a uma velocidade escalar de 30m / s . O motorista aciona os freios em A e, assim, reduz a velocidade escalar do carro a uma razão de a t = - t / 8m / s 2 , onde t é dado em s . D
2/115) Na parte inferior A da acrobacia aérea na qual o avião descreve um círculo em um plano vertical , o módulo da aceleração total do avião é de 3 g . Se a velocidade do avião em relação ao ar é de