Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Medidas de Dispersão

Ver Teoria
Exercício 12345678910

Enunciado

Será mera coincidência?

Considere o seguinte conjunto de dados:

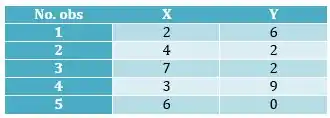
a) Calcule as variâncias amostrais de X e de Y, ou seja, S x 2   e   S Y 2

b) Construa uma nova variável Z = X + Y e calcule a sua variância amostral S z 2

c) Compare S z 2 com S x 2 + S y 2 + 2 S x y

d) Como você explica essa coincidência?

Passo 1

Queremos a Variância Amostral, portanto vamos usar:

s 2 = ∑ x i 2 - n . x ¯ 2 n - 1

Temos que:

x ¯ = ∑ i = 1 n x i n

Passo 2

  • Para X:

    • x - = 2 + 4 + 7 + 3 + 6 5 = 22 5 = 4,4

    Logo

    S x 2 = 2 2 + 4 2 + 7 2 + 3 2 + 6 2 - 5 × 4,4 2 5 - 1 = 114 - 5 × 19,36 4 = 17,2 4

    S X 2 = 4,3

    Passo 3

  • Para Y:

    • y - = 6 + 2 + 2 + 9 + 0 5 = 19 5 = 3,8

    Logo

    S Y 2 = 6 2 + 2 2 + 2 2 + 9 2 + 0 2 - 5 × 3,8 2 5 - 1 = 125 - 5 × 14,44 4 = 52,8 4

    S Y 2 = 13,2

    Passo 4

    b) Construa uma nova variável Z = X + Y e calcule a sua variância amostral S z 2

  • Para Z:

z - = 8 + 6 + 9 + 12 + 6 5 = 41 5 = 8,2

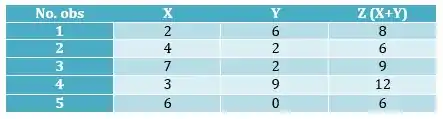
Logo

S Z 2 = 8 2 + 6 2 + 9 2 + 12 2 + 6 2 - 5 × 8,2 2 5 - 1 = 361 - 5 × 67,24 4 = 24,8 4 = 6,2

Passo 3

c) Compare S z 2 com S x 2 + S y 2 + 2 S x y

Agora vamos comparar o resultado obtido em S Z 2 com essa expressão dada.

Lembre-se que S X Y = C o v ( X , Y ) e que por sua vez

C o v X Y = ∑ i = 1 n x i y i - n x - y -   n - 1

Vamos calcular então S X Y :

C o v X Y = ∑ i = 1 n ( x i y i - n x - y - )   n - 1

= [ 2 × 6 + 4 × 2 + 7 × 2 + 3 × 9 + 6 × 0 - 5 4,4 × 3,8 ] 4

C o v X Y = S X Y = 61 - 83,6 4 = - 5,65

Então teremos:

S X 2 + S Y 2 + 2 S X Y = 4,3 + 13,2 + 2 × - 5,65 = 17,5 - 11,3 = 6,2

Ou seja,

S X 2 + S Y 2 + 2 S X Y = S Z 2

Passo 4

d) Como você explica essa coincidência?

Essa coincidência não é tããão coincidência assim. Se antes tínhamos a seguinte propriedade:

V a r X + Y = V a r X + V a r Y + 2 C o v ( X Y )

Agora temos na versão amostral

S X 2 + S Y 2 + 2 S X Y = S X + Y 2

Resposta

a)   17,2 4 e 52,8 4

b) 6,2

c) S X 2 + S Y 2 + 2 S X Y = S Z 2

d) Se antes tínhamos a mesma relação para as variâncias, teremos para as variâncias amostrais.

Exercícios de Livros Relacionados

Nos exercícios 29 e 30, use a Regra Empírica.O valor médio da TV via satélite de uma amostra de domicílios era de $70,00 por mês com desvio padrão de $14,50 por mês. Entre quais dois valores encontram
De uma amostra aleatória de domicílios, listamos o número de aparelhos de televisão. Encontre a média e o desvio padrão amostral dos dados.Números de televisores 0 1 2 3 4 5Números de domicílios 1 8 1
Raciocínio gráfico. Compare os três conjuntos de dados. (a) Sem calcular, determine qual conjunto de dados tem o maior desvio padrão amostral e qual tem o menor. Explique seu raciocínio.(b) De que man
Por que o desvio padrão é usado com mais frequência do que a variância?
Encontrando estatísticas amostrais. Encontre a amplitude, a média, a variância e o desvio padrão para a amostra dada.Tempo de gestação. A duração (em dias) da gravidez para uma amostra aleatória de mã