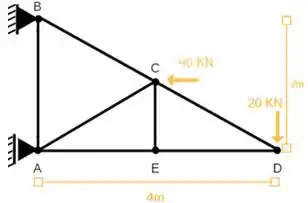
Calcule as reações de apoio e as forças normais nas barras através do Método dos Nós. Dado: Ângulo(cae) = ângulo(cde) = 26,57°
Passo 1
Nosso primeiro passo vai ser entender o enunciado, de acordo com enunciado, precisamos encontrar todas as forças normais em todas as barras. Para isso agora precisamos determinar, quais são as reações existentes na treliça! Vamos lá?
Começamos, desenhando em vermelho todas as reações existentes que são realizadas pelos apoios. São elas:
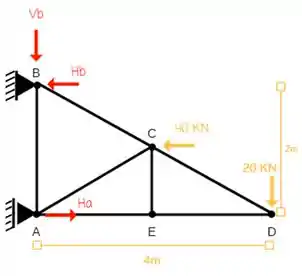
Não se esqueça, quando temos um apoio de primeiro gênero como o do ponto A, temos apenas esforço na vertical e quando temos um apoio de segundo gênero como o do ponto B, teremos esforço na horizontal e na vertical!Mais uma dica importante, você pode arbitrar a o sentido das forças como achar melhor ou até mais bonitinho, rs!
Pois caso você escolha uma direção e ela esteja errada, você vai encontrar no final o resultado com uma resposta negativa, e na mecânica resultados negativos caracterizam, que a direção é ao contrário do que arbitrou inicialmente!
Agora, podemos verificar a Isostática da treliça, segundo a fórmula:
Onde n = 5 pois temos os nós A,B,C,D e E;
b = 7, pois temos sete barras;
v = 3 , pois temos três reações nos apoios.
Assim,
Passo 2
Agora é a hora calcular as reações de apoio.
Vamos usar as condições para a treliça estar em equilíbrio, lembrando são elas;
Somatório dos momentos em relação a um ponto igual a zero!
Somatório das forças verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Mais uma dica importante,
Passo 3
Agora iremos Anlisar cada Nó da treliça.
Vamos começar analisando o nó B;
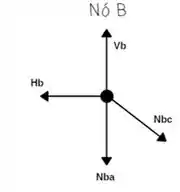
Somatório das forças Horizontais igual a zero!
Somatório das forças verticais igual a zero!
;
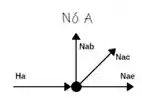
Somatório das forças verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Agora vamos analisar o nó E;
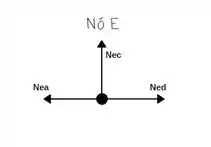
Somatório das forças Horizontais igual a zero!
Somatório das forças verticais igual a zero!
Agora vamos analisar o nó C;
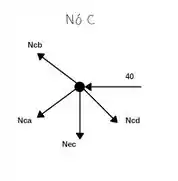
Somatório das forças Horizontais igual a zero!
(Dica importante, quando começarmos a chegar em equações que destinem como igualdade 0 = 0, significa que estamos próximos de já conhecer todas as reações existentes na treliça)
Somatório das forças verticais igual a zero!
Agora vamos analisar o nó D;
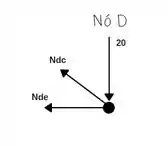
Somatório das forças Horizontais igual a zero!
Somatório das forças verticais igual a zero!