Para a treliça a seguir, determinar seus esforços em cada barra. Indique as barras que estão tracionadas ou comprimidas.
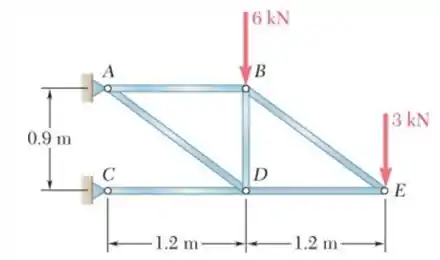
Passo 1
Nosso primeiro passo é entender o enunciado e pensar na melhor maneira de solucionar a questão!!
Como o nosso enunciado já diz, precisaremos determinar os esforços em cada barra! Certo?Para isso vamos precisar pensar qual seria o melhor método para resolver a questão... Pensou nisso também? É isso mesmo, iremos usar o método dos nós, isolar os nós para poder descobrir cada uma das forças, uma dica muito irada é que quase sempre que precisarmos encontrar todas as reações em cada barra, precisaremos usar o método dos nós.
Então bora lá usar o método dos nós...
Uma boa observação, é você perceber que a princípio as reações do apoio não vão influenciar nas contas para encontrar as reações das barras! Por isso iremos começar isolando o ponto oposto aos apoios!
Passo 2
Vamos isolar então o ponto E da treliça;
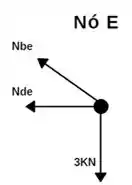
Um detalhe importante, como podemos ver a força Nbe não está alinhada nos eixos, por isso vamos precisar decompor ela!Para isso precisamos saber o seno e o cosseno do ângulo entre Nbe e Nde.
Vamos chamar esse ângulo de Ѳ, assim podemos afirmar que atráves das medidas das barras;Assim,
Temos , agora partiu aplicar as fórmula de equilíbrio???
Vamos lá...
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 3
Próximo nó que podemos isolar é o nó B;
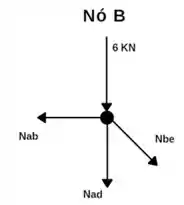
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 4
Próximo nó que podemos isolar é o nó D;
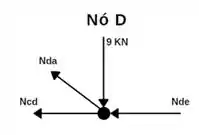
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Resposta
Todas as forças positivas são forças de tração e todas as forças negativas são forças de compressão.