a) Determine as forças normais nas barras da treliça da figura abaixo.
b) Sabendo que as barras desta treliça se rompem para forças de compressão de 100 KN e para forças de tração de 200 KN, determinar o valor de P que levaria essa treliça a ruptura.
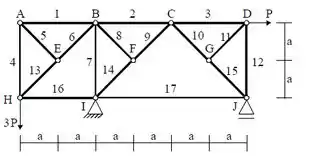
Passo 1
Esse exercício é separado em duas partes, então vamos começar resolvendo a letra (a) e depois vamos para (b), de forma a ficar mais claro, como resolver!
Bom na letra (a), precisamos usar o método dos nós para poder encontrar todas as reações presentes nas barras da treliça.
Vamos começar marcando as reações dos apoios, são elas:
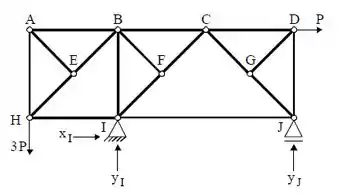
Agora vamos utilizar o equilíbrio da treliça;
Somatório dos momentos em relação ao ponto I:
Somatório das forças horizontais igual a zero:
Somatório das forças verticais igual a zero:
Passo 2
Para esse tipo de exercício, podemos utilizar um macete para facilitar nossas contas, como pudemos perceber as treliças estão meio que todas com a mesma inclinação, podemos tentar rotacionar nosso eixo de referencial para facilitar as contas!
Seguindo essa linha de pensamento, podemos começar pelo Nó E, que é um nó central ao quadrado ABIH, e aí poderemos observar que:
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Seguindo essa mesma linha de raciocínio, teremos no Nó F;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Seguindo essa mesma linha de raciocínio, teremos no Nó G;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Seguindo essa mesma linha de raciocínio, teremos no Nó A;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Seguindo essa mesma linha de raciocínio, teremos no Nó D;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 3
Agora, iremos observar nós um pouco mais complexos, como o Nó H;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Agora o nó B;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Agora o nó I;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Agora o nó J;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 4
Resolvendo a letra (b)
Precisamos entender o seguinte, a treliça se rompe em duas condições:
A primeira, é se as barras sofrerem uma compressão de no máximo 100 KN e a segunda se tração for de no máximo 200 KN.
Então precisamos pensar no seguinte!
De todas as barras que sofrem compressão (+), qual é a maior? Concorda comigo que é são as barras 7 ou 16. Assim,
De todas as barras que sofrem compressão (+), qual é a maior? Concorda comigo que é são as barras 6 ou 13. Assim,
32P=100P=47,14 K
Dessa forma, podemos concluir que a treliça se rompe para P = 33,33 K
Resposta
(a)
N1 = 0 KN
N2 = 3P KN
N3 = P KN
N4 = 0 KN
N5 = 0 KNN6 = 3P KN
N7 = -3P KN
N8 = 0 KN
N9 = -P KNN10 = P KNN11 = 0 KNN12 = 0 KNN13 = 3P KNN14 = -P KNN15 = P KNN16 = -3P KNN17 = -P KN
(b) A barra se rompe para P = 33,33 KN