Determine as forças normais nas barras na treliça dada:
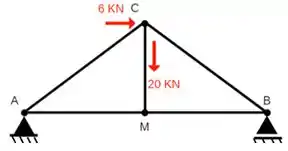
Dados : AB = 4 m, M é ponto Médio, MC = 1,5 m e Ângulo(cab) = Ângulo(abc) = α °
Passo 1
Vamos entender o enunciado...
De acordo com enunciado, precisamos encontrar todas as forças em todas as barras.
Porém para isso, precisamos descobrir o valor do ângulo α°, pois precisaremos dele para fazer projeções das forças normais nas barras AC e BC.

Para isso iremos precisar lembrar de nossas fórmulas de ensino médio... mais conhecidos como bons tempos!
Usaremos relações métricas no triângulo retângulo ACM:
Passo 2
Agora precisamos determinar, quais são as reações existentes na treliça! Vaaaamos?
Começamos, desenhando em rosa todas as reações existentes que são realizadas pelos apoios.
São elas:
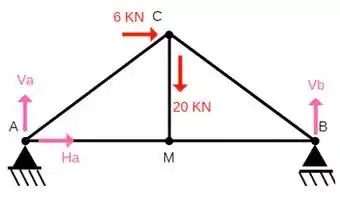
Super Dica: Precisamos sempre lembrar que quando temos um apoio de primeiro gênero como o do ponto B, temos apenas esforço na vertical, e quando temos um apoio de segundo gênero como o do ponto A, teremos esforço na horizontal e outro na vertical!Vale lembrar também que, você pode arbitrar a o sentido das forças como você preferir, caso você escolha uma direção e ela esteja errada, você vai encontrar no final o resultado com uma resposta negativa!
Na mecânica resultados negativos caracterizam, que a direção é ao contrário do que arbitrou inicialmente!
Agora, podemos verificar a Isostática da treliça, segundo a fórmula:
Onde n = 4 pois temos os nós A,B ,C e M;
b = 5, pois temos cinco barras;
v = 3, pois temos três reações nos apoios.
Assim,
Passo 3
Agora que provamos que a treliça é isostática, é a hora calcular as reações de apoio.
Vamos usar as condições para a treliça estar em equilíbrio, lembrando são elas;
Somatório dos momentos em relação ao ponto A igual a zero! (Aqui nós iremos arbitrar como ;positivo os momentos que seguirem no sentindo horário em relação ao relógio). Assim.
-
Somatório das forças verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Passo 4
Agora iremos Anlisar cada Nó da treliça.
Vamos começar analisando o nó A;
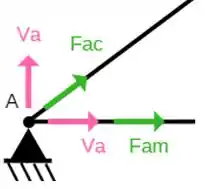
Somatório das forças verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Agora escolhemos o ponto B por ter menos reações:
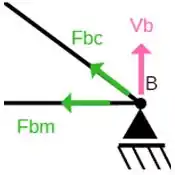
Somatório das forças Verticais igual a zero!
Somatório das forças Horizontais igual a zero!
Agora podemos observar que