A treliça abaixo pode ser considerada uma treliça simples. Usando seus conhecimentos sobre treliças determine
- Quais os 2 primeiros nós que devemos resolver
- Qual a ordem de nós a serem resolvidos
- O valor do normal em todas as barras da treliça
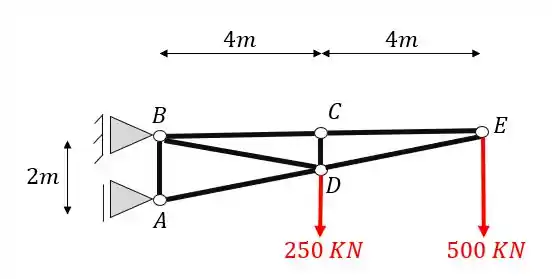
Passo 1
Para resolver os problemas sobre treliças precisamos seguir uma sequência de passos que facilita a resolução, em que temos que respeitar o seguinte
- Primeiro devemos calcular as reações de apoios da nossa treliça, que será calculada levando em consideração dois fatores
- A segunda coisa que devemos analisar nesse exercício é o melhor nó, e para isso temos que lembrar que no equilíbrio de nós sempre iremos usar as seguintes equações
- A terceira coisa que devemos ver é que sempre que resolvemos uma barra, tiramos uma incógnita do nosso problema, ou seja, se tivermos nós que compartilhem a mesma barra, pro nó ainda a ser resolvido, a barra compartilhada com ele o ajudará a calcular as desconhecidas, sempre, é claro, respeitando a regra de duas barras desconhecidas por nó, como vimos na teoria.
As reações

E as equações de equilíbrio
Ou seja, se temos duas equações, só podemos ter duas incógnitas para resolver o nosso nó.
Como cada barra representa uma incógnita, e que pelo passo anterior já teremos calculado as reações de apoio, sabemos que as únicas incógnitas serão as barras, e lembre-se, se cada barra é uma incógnita, e eu só posso ter duas incógnitas por nó, os melhores nós para iniciarmos serão aqueles que tem duas barras.
Se seguirmos esse último passo ao pé da letra, conseguiremos resolver tranquilamente todas as barras de uma treliça.
Agora que já conhecemos os três passos da nossa solução, vamos aplicar eles ao nosso problema.
Passo 2
A primeira coisa que devemos fazer como vimos no nosso passo a passo é definir as reações de apoio. Para isso devemos primeiro determinar os vetores reações de apoio e lembrar que sempre consideramos a nossa treliça como um elemento solido e único que usamos para determinar essas reações, com isso teremos que o nosso diagrama de corpo livre será
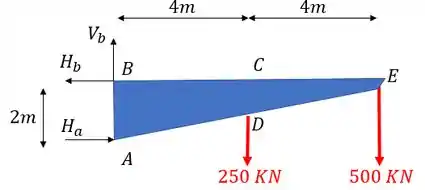
Definido os vetores reações de apoio já podemos usar as fórmulas de equilíbrio
Substituindo
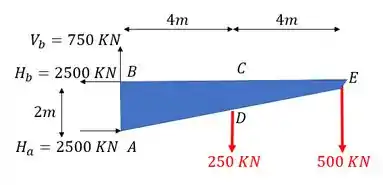
Assim já cumprimos a primeira parte do nosso passo a passo.
Passo 3
Agora que já cumprimos a primeira parte, precisamos fazer a segunda parte, que consiste em definir os melhores nós a serem calculados, e o valor do normal nas barras desses nós.
Como vimos anteriormente, os melhores nós para iniciarmos são aqueles que possuem somente duas barras, já que como vimos, cada nó só pode ter duas barras desconhecidas.
Com isso a nossa barra tem que os melhores nós que ela possui para iniciarmos os cálculos são
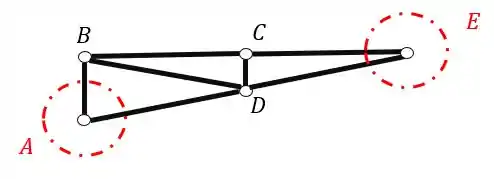
Pois são os únicos nós que possuem somente duas barras, logo, são os melhores para iniciarmos.
Passo 4
Agora precisamos fazer o equilíbrio dos nós, vamos começar pelo nó A.
Sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo

A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
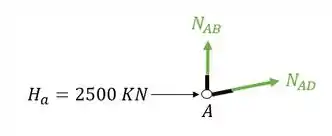
A terceira coisa que devemos fazer é definir o seno e o cosseno do ângulo entre as barras, pra isso usaremos as medidas dadas na nossa treliça
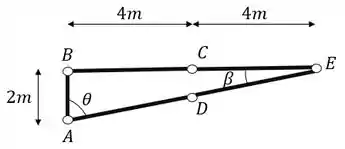
Sabemos que podemos calcular o nosso ângulo pela tangente, dessa forma teremos
Qual ângulo tem tangente igual a 4?
Agora já conseguimos decompor os nossos normais, já que já temos os ângulos, vamos calcula-los então.
Passo 5
Vamos lá então, decompondo os nossos normais teremos que
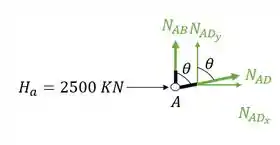
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
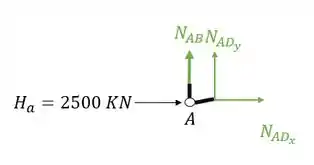
Sabemos que , substituindo teremos que
Logo
Substituindo no segundo sistema teremos
Então já calculamos os normais das barras do nó A.
Passo 6
Vamos agora calcular os normais do segundo nó, o nó E, sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo
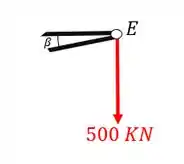
A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
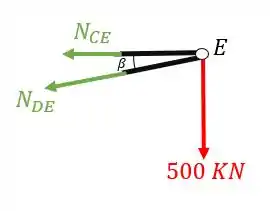
Agora já conseguimos decompor os nossos normais, já que já temos os ângulos, vamos calcula-los então.
Passo 7
Vamos lá então, decompondo os nossos normais teremos que
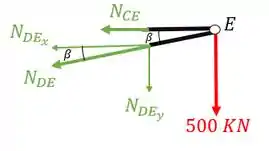
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
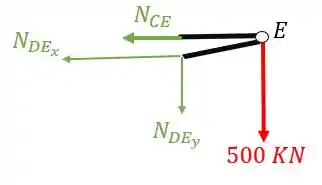
Sabemos que , substituindo teremos que
Logo
Substituindo no segundo sistema teremos
Então já calculamos os normais das barras do nó E.
Passo 8
Marcando de vermelho na nossa treliça as barras calculadas, teremos que
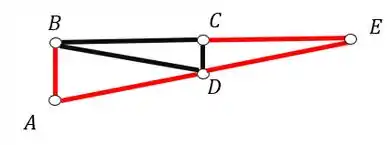
Perceba que o próximo nó a ser escolhido, só pode no máximo ter 2 barras desconhecidas, caso contrário, não conseguiremos calcular essas barras, porém, se prestarmos bem a atenção, veremos que todos os nós que faltam(B, C e D) possuem apenas duas barras desconhecidas (barras pretas), dessa forma podemos escolher qualquer um desses nós que faltam para fazermos o equilíbrio.
Como o nó C é composto apenas de barras perpendiculares, irei escolher esse nó para prosseguirmos o cálculo.
Passo 9
Sabemos que a primeira coisa que devemos fazer é isolar o nó como vemos abaixo
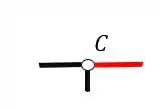
A segunda coisa que devemos fazer é colocar os normais saindo das barras cortadas
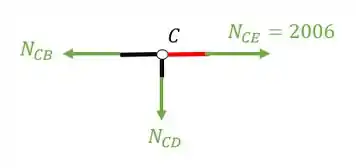
Substituindo e fazendo o equilíbrio teremos que
Então já calculamos os normais das barras do nó C.
Passo 10
Agora falta apenas a barra BD, vamos fazer o equilíbrio do nó B
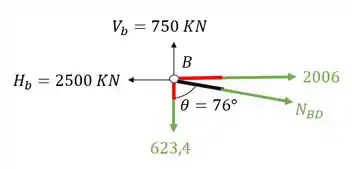
Decompondo os nossos normais teremos que
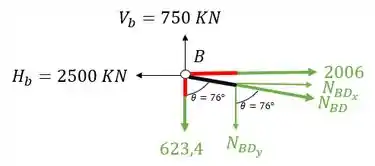
Fazendo a decomposição teremos que
Substituindo e fazendo o equilíbrio teremos que
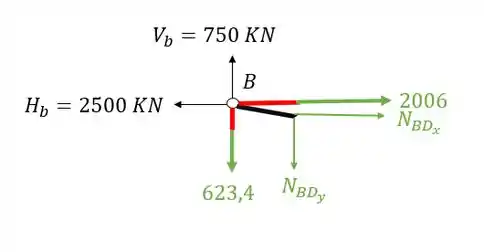
Substituindo teremos que
Logo
Com isso calculamos o normal de todas as barras que precisávamos, resolvendo assim a questão.
Resposta
Os Normais são