Determine as reações nos apoios e . Considere constante.
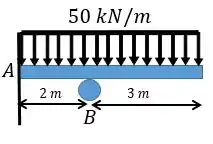
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas. Lembrando que vamos seguir o procedimento:
- Transformar o apoio em uma força e dividir os carregamentos.
- Elaborar os diagramas .
- Analisar as condições de contorno da linhas elástica.
- Utilizar o métodos dos momentos de área para calcaular uma reação.
- Com o valor dessa reações calcular as demais.
Passo 2
Vamos começar transformando o carregamento:
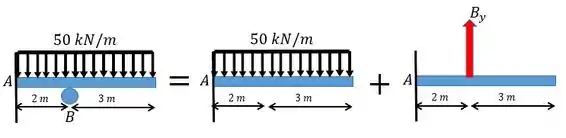
Perceba que não mudamos o carregamento, apenas segregamos em diferentes figuras e retiramos o apoio e o substituímos por uma força que é a força de reação.
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
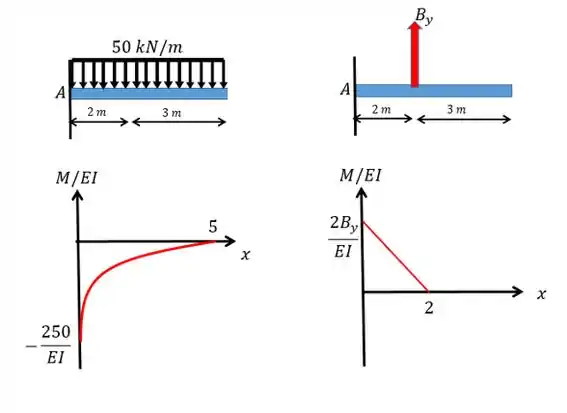
Passo 4
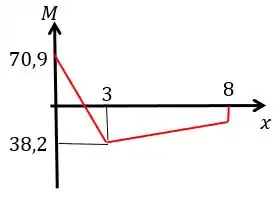
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar o valor de .
A gente tem que saber como vai ser a configuração da linha elástica e principalmente as condições de contorno. Abaixo vamos representar um esboço da linha elástica:
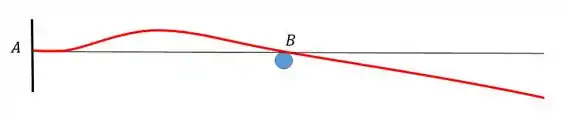
As condições são as seguintes:
No engaste :
Na rótula
Passo 5
Agora vamos utilizar essas condições de contorno para achar o valor de vamos fazer isso utilizando o método dos momentos das áreas para a linha neutra.
Repare que queremos a deflexão de em relação à , , que vai ser dada pelas áreas das figuras formadas nos seguintes gráficos:
- O primeiro é um triângulo então não tem muito segredo, basta lembrar que estamos olhando da perspectiva do ponto então as distâncias serão a partir desse ponto:
- Já para o segundo gráfico temos uma parábola. Assim como no anterior a perspectiva é sobre o ponto , mas vale ressaltar que a área e o centro de massa de uma parábola deste tipo são:
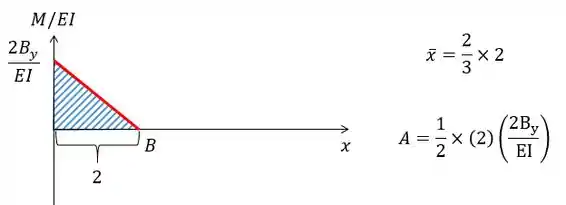
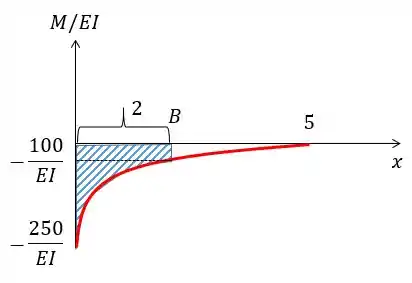
Como a nossa parábola não está completa vamos fazer o total (de 0 a 5) menos a parte branca (de 2 a 5).
Como temos mais de uma figura:
Lembre-se que o ponto que estamos analisando está centrado em , logo, todas as distâncias são referentes a esse ponto.
Como, pelas condições de contorno a deflexão em é igual à deflexão em vamos ter que:
Sendo assim,
Passo 6
Agora é só utilizar as equações da estática para achar o resto das reações, fazendo o diagrama de corpo livre:
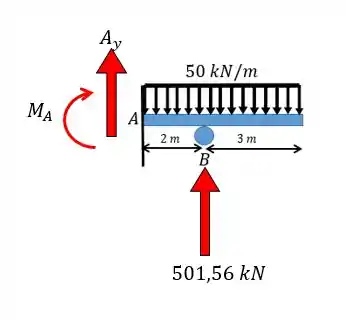
Podemos ver que:
Resposta