Determine as reações nos apoios e . Considere constante.
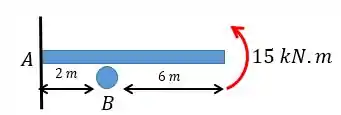
Passo 1
Faaala, galera!!! E aí como vocês estão, prontos para começarem uns exercícios de método dos momentos de áreas aplicado a vigas estaticamente indeterminadas? Tenho certeza que sim!!!
Vamos lá, então pessoal! Como o próprio tópico já diz estamos falando de vigas estaticamente indeterminadas, isso significa dizer que as reações das vigas não podem ser calculadas com base apenas nas equações da estática, logo a gente vai precisar de mais uma ferramenta para isso.
Essa ferramenta é o diagrama aliado com um certo conhecimento da linha elástica. Vamos ver como isso nos ajudará!!
Passo 2
Vamos começar transformando o carregamento em dois carregamentos mais simples:
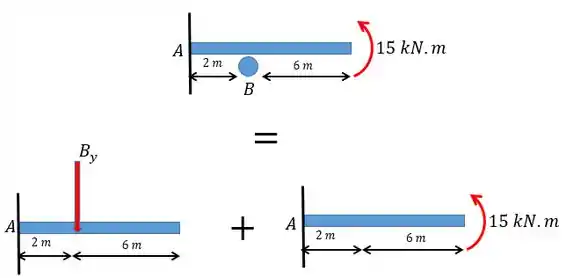
Perceba que não mudamos o carregamento! A única coisa que fizemos foi tirar o apoio e aplicar uma força que é a força de reação.
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
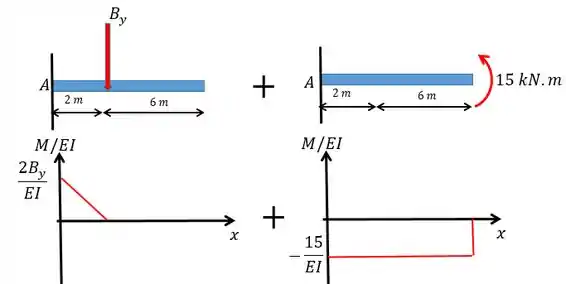
Passo 4
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar o valor de .
A gente tem que saber como vai ser a configuração da linha elástica e principalmente as condições de contorno. Abaixo vamos representar um esboço da linha elástica:
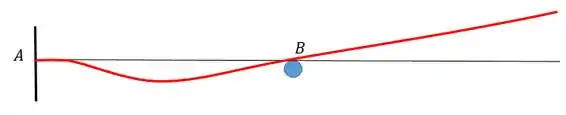
As condições são as seguintes:
No engaste :
Na rótula
Passo 5
Agora vamos utilizar essas condições de contorno para achar o valor de vamos fazer isso utilizando o método dos momentos das áreas para a linha neutra.
Repare que queremos a deflexão de em relação à que vai ser dada pelas áreas das figuras formadas nos gráficos:
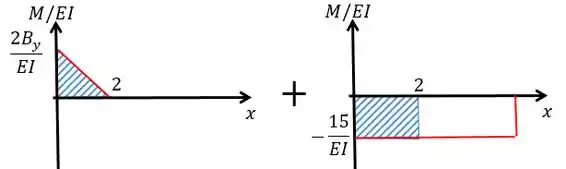
Como temos mais de uma figura:
Como, pelas condições de contorno a deflexão em é igual à deflexão em vamos ter que:
Sendo assim,
Passo 6
Agora é só utilizar as equações da estática para achar o resto das reações, fazendo o diagrama de corpo livre:
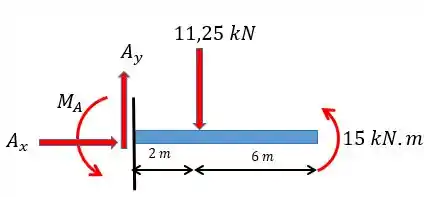
Podemos ver que: