Determine as reações nos apoios. Considere constante.
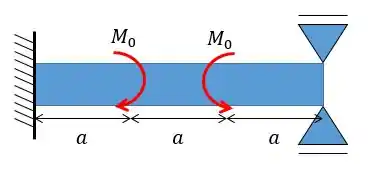
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas. Lembrando que vamos seguir o procedimento:
- Transformar o apoio em uma força e dividir os carregamentos.
- Elaborar os diagramas
- Analisar as condições de contorno da linhas elástica
- Utilizar o métodos dos momentos de área para calcaular uma reação
- Com o valor dessa reações calcular as demais.
Passo 2
Vamos começar montando o diagrama de corpo livre:
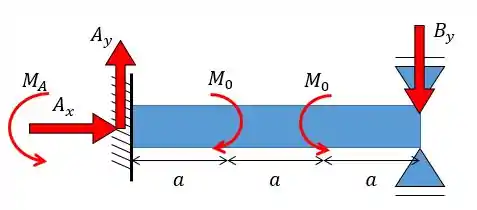
Agora vamos aplicar as equações da estática:
- Forças horizontais
- Forças verticais
- Momento
Porém, percebam que temos mais incógnitas do que equações logo vamos utilizar nosso conhecimento de linha elástica para achar mais uma equação!
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
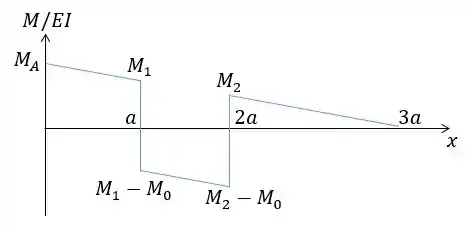
Onde:
Então vamos ter:
Passo 4
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar a nossa próxima equação!
Para isso vamos utilizar as condições de contorno que são:
No engaste :
No apoio
Então uma coisa que podemos fazer é aplicar a equação do momento de área entre os pontos e e assim vamos achar a deflexão relativa entre eles. Lembrando:
E o gráfico vai ser:
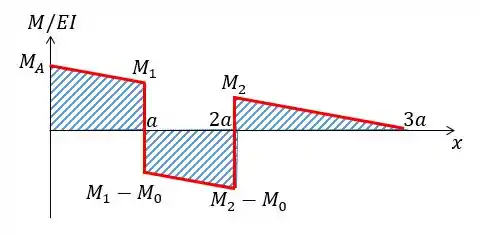
Passo 5
Agora vamos aplicar a equação fornecida no passo anterior e achar a deflexão relativa. Eu gosto de ao invés de trabalhar com trapézios sempre trabalhar com um retângulo mais um triângulo beleza? Então nós vamos ter 5 figuras:
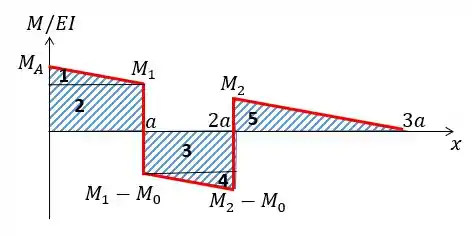
Como temos mais de uma figura:
Lembre-se que o ponto que estamos analisando está centrado em , logo, todas as distâncias são referentes a esse ponto.
- Para a figura número 1:
- Para a figura número 2:
- Para a figura número 3:
- Para a figura número 4:
- Para a figura número 5:
Agora temos de somar os 5 termos e obter:
Como ambos os pontos possuem deflexão igual a zero então vamos ter:
Logo,
Passo 6
Agora é só utilizar essa equação que achamos em conjunto com as outras três do início do problema que vamos encontrar todas as reações:
Um modo de resolver é colocar todos os termos em função de :
Resolvendo essa equação vamos encontrar: