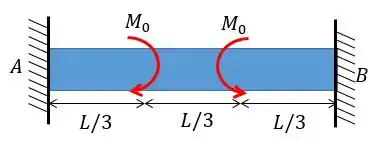
Determine as reações ao momento nos apoios e ; a seguir trace os diagramas de força cortante e momento fletor. é constante.
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas.
O primeiro passo vai ser sempre o mesmo, colocar as reações dos apoios e montar o nosso querido diagrama do corpo livre:
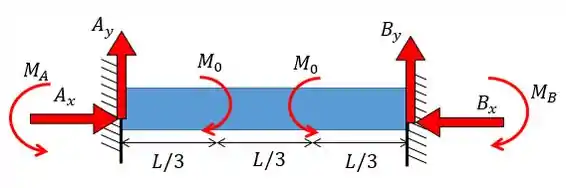
Repara que aqui, nós temos 6 incógnitas que são as reações nos nossos apoios, com isso, precisaríamos de 6 equações para determinar essa viga.
Mas repara só no seguinte, os momentos aplicados na nossa viga possuem o mesmo valor e estão aplicados em pontos simétricos, portanto, podemos dizer que há uma simetria na nossa viga.
Por isso,
Como não existem esforços verticais nem horizontais, não haverá reações nessas direções, portanto:
Com isso, ficamos apenas com duas incógnitas ( e) e uma equação (somatório dos momentos), o que resulta em problema estaticamente indeterminado e para resolve-lo, vamos seguir o passo-a-passo!
- Determinar as equações da estática
- Elaborar os diagramas
- Analisar as condições de contorno das linhas elásticas
- Utilizar o métodos dos momentos de área para calcular uma reação
- Com o valor dessas reações calcular as demais.
Passo 2
Vimos no Passo 1, que só iremos usar a equação do somatórios dos momentos que nesse caso, será:
- Momento
E como sabemos que o é zero, teremos então:
Logo, precisamos de apenas mais uma equação para resolver o problema e essa equação é a da linha elástica!
Passo 3
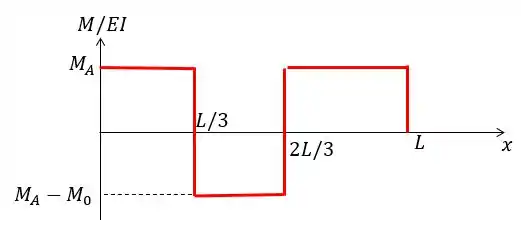
Agora a gente vai fazer o diagrama , a gente vai fazer isso somando os diagramas de cada carregamento.
Lembrando que vamos adotar aqui o sentido anti-horário como positivo!
Vamos começar nosso gráfico com o momento igual à que é o momento do engaste em . Ao chegar em , subtraímos com o momento dado pelo carregamento nesse ponto que é no sentido horário.
Depois, ao chegar em , somamos novamente o , pois agora o carregamento está no sentido anti-horário. E por fim, finalizamos o nosso gráfico, chegando em , quando subtraímos o momento , que sabemos que é igual a e por isso o nosso gráfico vai pra zero.
Passo 4
Beleza! A gente já tem os diagramas, agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar a nossa próxima equação!
Para isso vamos utilizar as condições de contorno que são:
No engaste :
No engaste
Então, uma coisa que podemos fazer é aplicar a equação do momento de área entre os pontos e e assim vamos achar a inclinação relativa entre eles. Lembrando:
Ah, e se liga, a inclinação relativa entre e vai ser zero, afinal e .
Vamos, encontrar agora essa área:
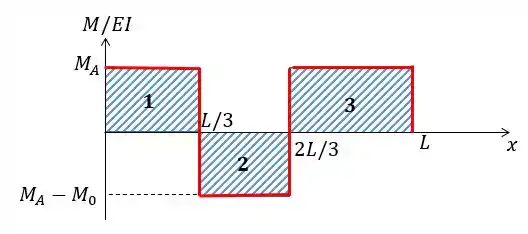
Agora é só fazer a área dessas figuras:
- Da figura número 1:
- Da figura número 2:
- Da figura número 3:
Passo 5
Então somando todos esses termos vamos ter:
Pessoal, normalmente quando uma área está localizada abaixa do eixo a gente tem que colocar um sinal negativo na sua frente, mas como o termo já é negativo, porque é maior do que então não vamos fazer isso nesse caso, beleza?
Mas a inclinação relativa entre e é zero, correto? Então vamos ter:
E sabemos que , logo:
Passo 6
Como o problema pede apenas as reações ao momento e vimos que:
Nós vamos ter como resultado: