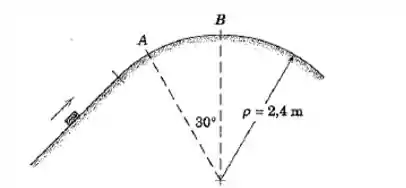
Se o bloco de passa sobre o topo da porção circular da trajetória com velocidade de , calcule o módulo da força normal exercida pela trajetória sobre o bloco. Determine a velocidade máxima que o bloco pode ter em sem que perca o contato com a trajetória.
Passo 1
Vamos calcular primeiro para o caso do enunciado:
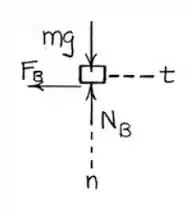
Assim, temos:
Passo 2
No outro caso:
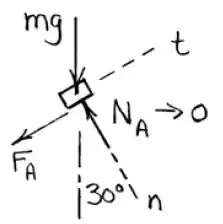
Como estamos estimando a velocidade para que o corpo perca o contato, devemos considerar que
Agora, precisamos apenas decompor a força peso na direção radial e comparar com a resultante:
Resposta
Exercícios de Livros Relacionados
Determine o coeficiente mínimo de atrito estático entre os pneus e a superfície da estrada de maneira que o carro de 1,5 Mg não deslize quando ele se move a 80 km/h na estrada em curva. Despreze a dim
Determine o coeficiente de atrito estático entre os pneus e a superfície da estrada é μ s = 0,25 , determine a velocidade máxima do carro de 1,5 Mg de modo que ele não deslize quando ele se move na cu
O dispositivo mostrado é usado para produzir a experiência de gravidade zero em um passageiro quando ele atinge o ponto A, θ = 90 ° , ao longo da trajetória. Se o passageiro tem massa de 75 kg, determ
Um acrobata tem peso de 750 N m ≈ 75k g e está sentado em uma cadeira que está fixada no topo de um mastro, como mostrado. Se por um acionamento mecânico o mastro gira para baixo com uma razão constan
O disco com a caneleta circular gira em torno do eixo vertical com uma rotação constante de 30r p m e suporta duas esferas de 4k g . Calcule a maior das duas forças de contato entre o disco e cada esf