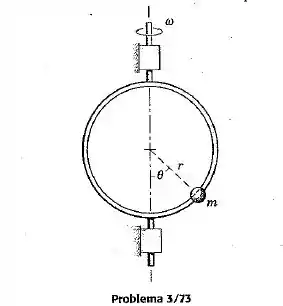
Uma pequena conta de massa é conduzida por um aro circular de raio que gira em torno de um eixo vertical fixo. Mostre como se pode determinar a velocidade angular do aro pela observaçaõ do ângulo que localiza a conta. Despreze o atrito em sua análise , mas assuma que uma pequena quantidade de atrito está presente para amortecer qualquer movimento da conta em relação ao aro uma vez que uma velocidade angular constante tenha sido estabelecida. Aponte quaisquer restrições sobre sua solução.
Passo 1
Vamos lá: Pelo enunciado sabemos que, ao atingir certa velocidade angular, a conta ficará numa posição “angular” fixa: aquele ângulo não vai mudar.
As forças que agem na conta são a força Normal e o Peso:
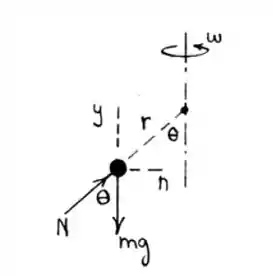
Pelo o equilíbrio vertical, temos:
Passo 2
Horizontalmente falando, temos uma resultante que é centrípeta. Assim:
Ai vem um pulo do gato. Lembra que Então:
Substituindo o valor de
Mas quem é , o raio de giração? Não é exatamente a , o raio do círculo, já que existe uma certa inclinação. Sendo assim:
Agora:
Pronto (:
Passo 3
Vamos pensar nas restrições agora: Veja que na solução existe um cosseno. Senos e cossenos sempre possuem uma restrição que é:
Assim:
Aplicando a restrição:
Resposta
Com