Uma câmara de possui uma bexiga cheia de gás perfeito a e . Essa bexiga possui uma resistência elétrica de em seu interior. Ao ligar essa resistência a uma fonte com de tensão por , o gás no interior da bexiga é aquecido até uma temperatura de . Por causa desse aquecimento, o gás se expande isobaricamente até estourar a bexiga e ocupar toda a câmara. Determine:
- a diferença entre o volume da câmara e o volume que a bexiga tinha logo antes de estourar;
- o trabalho total realizado pelo gás ao expandir dentro da bexiga e ao expandir por toda a câmara.
Passo 1
Como estão, chuchus?! Essa é uma questão que mistura dois temas: expansão não resistida e potência elétrica. Vamos resolver e ficar fera nesses assuntos?

Vamos sim, larga essa preguiça!
Primeiro, a questão quer saber quanto vale a diferença entre o volume da câmara e o volume que a bexiga tinha logo antes de estourar.
já foi informado pelo enunciado e vale . Logo, só resta encontrar pra calcular a resposta da letra (a) da questão. é encontrado, se a gente supor que toda a energia dissipada pela resistência elétrica é usada pelo gás para realizar o trabalho a pressão constante sobre a bexiga, fazendo ela crescer até estourar. A figura abaixo mostra isso.
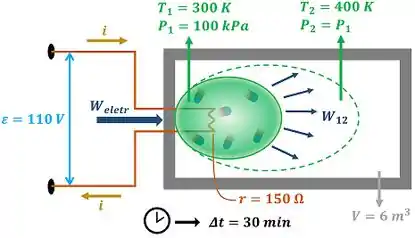
é a diferença de potencial elétrico da bateria, é a corrente elétrica que passa pelo circuito e é a resistência da lâmpada. e são a pressão e a temperatura do gás antes de expandir. e são a pressão e a temperatura do gás depois de expandir na bexiga.
Depois de tanta informação, vamos partir pra prática e resolver a letra (a)!
Passo 2
Como dito no passo 1, pra achar e calcular , temos que supor que a energia dissipada pela resistência é toda usada pra realizar um trabalho de movimento de fronteira sobre a bexiga. Logo, deve ser igual a .
Como é trabalho de movimento de fronteira a pressão constante, podemos calcular multiplicando a pressão pela variação de volume da bexiga . Além disso, o trabalho elétrico pode ser calculado multiplicando a potência elétrica pelo intervalo de tempo em que ela foi usada.
Para calcular , precisamos achar através da fórmula Pevetê Povotó de gases perfeitos.
Como , cortamos essas pressões e reorganizamos a equação pra achar .
Além disso, é igual a vezes . é encontrado através da lei de Ohm abaixo.
Vamos substituir todos esses dados na próxima etapa para achar e .
Passo 3
Substituindo as informações na segunda equação do passo 2:
Colocando em evidência:
Antes de substituir os valores, temos que converter a pressão de pra , multiplicando ela por e temos que converter de pra , multiplicando ele por
Substiuindo esse valor na equação de :
Essa é a resposta da letra (a). Então bora partir pra letra (b) e encerrar a questão!
Passo 4
O trabalho total é a soma do trabalho de expansão da bexiga e o trabalho de expansão do gás ao ocupar toda a câmara!
já pode ser encontrado pela fórmula abaixo.
Como o gás aumenta de volume e sua fronteira se expande, quando ele se difunde pela câmara, tendemos a achar que podemos calular o trabalho pela fórmula que calcula o trabalho de fronteira abaixo.
No entanto, usar essa fórmula é um erro, porque essa expansão devida ao rompimento da bexiga é uma expansão não resistida. Nesse caso, o gás não precisa vencer uma resistência para se expandir e ocupar o volume que estava em vácuo! Logo, o gás não precisa gastar energia e realizar trabalho para se mover. Ou seja, o trabalho que ele realiza vale !
Por isso, vale:
Ebaaaaaaa! Terminamos a questão! Encontramos a resposta da letra (b)!