O conjunto cilindro-pistão mostrado na figura abaixo possui um membrana em seu interior. Essa membrana separa a parte interna do cilindro em duas partes. Uma parte com de volume contém um gás perfeito a e um gás perfeito. A outra parte com de volume está em vácuo absoluto. A membrana é rompida, fazendo o gás se expandir isotermicamente no cilindro. Ao fim dessa expansão, os pinos que travam o pistão são removidos, permitindo que o gás aumente isobaricamente seu volume em . Determine o trabalho total exercido pelo gás ao longo dessas duas expansões.
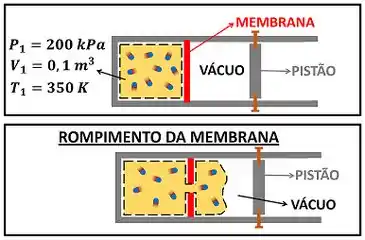
Passo 1
Oi, gente boa! Como está a vida?

Vamos exercitar os conhecimentos téoricos, fazendo uma questão de expansão não resistida?
A questão quer que a gente calcule o trabalho total relacionado a dois processos de expansão que o gás sofre. A primeira expansão faz o gás ir do estado 1 pro 2, realizando um trabalho . No segundo processo, o gás vai do estado 2 pro 3, realizando um trabalho .
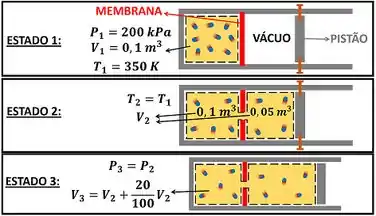
O trabalho total é justamente a soma desses dois trabalhos que o gás realiza ao se expandir.
No primeiro processo, a membrana se rompe e faz o gás se expandir com temperatura constante do estado 1 pro estado 2. No segundo processo, o gás empurra o pistão e se expande a pressão constante do estado 2 pro estado 3.
Com todas essas informações em mãos, vamos começar a questão tentando calcular .
Passo 2
Quando a membrana se rompe, o gás tende a se expandir e ocupar o volume de que antes era apenas vácuo! Dessa forma, seu volume que antes valia cresce e passa a valer .
Como o gás aumenta de volume e sua fronteira se expande, tendemos a achar que podemos calular o trabalho pela fórmula que calcula o trabalho de fronteira abaixo.
No entanto, usar essa fórmula é um erro, porque essa expansão devida ao rompimento da membrana é uma expansão não resistida. Nesse caso, o gás não precisa vencer uma resistência para se expandir e ocupar o volume que estava em vácuo! Logo, o gás não precisa gastar energia e realizar trabalho para se mover. Ou seja, o trabalho que ele realiza vale !
Pronto! Achamos o trabalho do primeiro processo de expansão. Resta apenas conhecer o valor de para achar e acabar com a questão!
Passo 3
O segundo processo de expansão é o processo do gás empurrando um pistão para se expandir. Ou seja, nesse caso, o gás precisa gastar energia para vencer a força contrária que o pistão faz. Logo, esse segundo processo se trata de um processo de trabalho de movimento de fronteira. Como ele é um processo isobárico, podemos usar a equação abaixo.
Já sabemos o valor de . Precisamos achar e . é calculado, lembrando que o volume do gás aumenta em nesse segundo processo de expansão.
Com esse dado, já poderemos calcular e na próxima etapa!
Passo 4
Achamos a partir de . Pra isso, lembramos que o primeiro processo de expansão era a temperatura constante. Logo . Usando a fórmula de gases perfeitos Pevetê Povotó, achamos:
Cortando e dos dois lados da equação:
Reorganizando a equação:
Substituindo na equação de :
Substituindo na equação de :
Aí siiiiiimmmm! Mais um exercício resolvido! Bora aproveitar o pique pra fazer mais um?