Uma certa quantidade de vapor de água saturado a é condensada isotermicamente para líquido saturado em um arranjo pistão-cilindro.
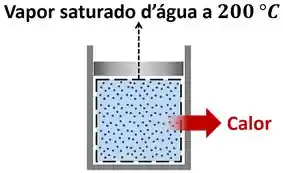
Calcule a transferência de calor e o trabalho realizado durante esse processo, em . Use a tabela de propriedades termodinâmicas abaixo.
Passo 1
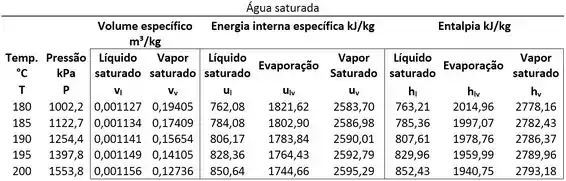
O exercício diz que um sistema passa por um processo com troca de calor e trabalho. O sistema é formado inicialmente por vapor d’água a (estado 1). Depois de trocar calor e trabalho, o sistema vira líquido saturado (estado 2). A figura abaixo mostra o sistema antes e depois do processo.
A figura mostra que conforme o vapor vai perdendo calor e condensando, o pistão vai descendo. Isso significa que o volume do sistema vai diminuindo, porque a sua fronteira vai descendo junto com o pistão. Ou seja, além do pistão trocar calor, a vizinhança realiza trabalho sobre ele. E não é qualquer tipo de trabalho! É um trabalho de movimento de fronteira .
Mas como podemos resolver essa integral para calcular o trabalho?
Lembrando que durante uma condensação isotérmica a pressão também não muda!

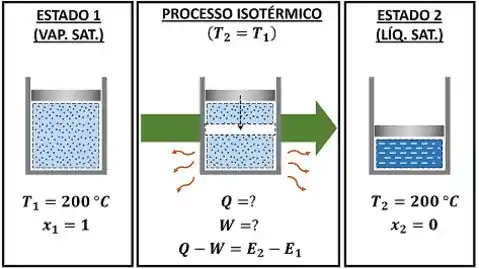
Ou seja, além do processo manter a temperatura constante, ele também mantém a pressão constante. Isso é mostrado na figura abaixo, comparando a pressão do estado condensado B com a pressão do estado vaporizado D. A pressão B é igual à pressão D. Isso fica mais claro quando a gente olha para o gráfico -.
Por causa disso a fórmula do trabalho vira:
onde:
- é o volume inicial do sistema;
- é o volume final do sistema;
- é a pressão do sistema. Ela é constante durante todo o processo.
E como conseguimos achar essas três propriedades?
Vamos por partes! Primeiro vamos começar pela pressão . Ela é encontrada através da tabela de saturação da água. Ela é a pressão de saturação da água para a temperatura de .
Para encontrar os volumes, temos que lembrar que eles dependem da massa do sistema:
onde:
- é o volume específico do vapor saturado de água a . Ele é encontrado na tabela de saturação;
- é o volume específico da água líquida saturada a . Ele também é encontrado na tabela de saturação.

E a massa do sistema ? Como achamos?
Nós não precisamos dela!
O exercício pede para encontrarmos o trabalho em , porque ele não pede , mas sim dividido por .
Olhando para a equação de cima, descobrimos que já temos todas as informações que precisamos para achar o resultado pedido.
Mas e a troca de calor dividida pela massa ? Como podemos calculá-la?
Isso fica para o próximo passo!
Passo 2
Para calcular teremos que usar a primeira lei da termodinâmica.
Nós já sabemos como calcular o trabalho, mas como a gente pode calcular a variação de energia total , se a tabela de propiedades só tem valores de energia interna específica ?

A primeira etapa para a gente saber como calcular a variação de é olhar para a equação de energia total.
onde:
- é a massa do sistema;
- é a energia interna específica. Ela é encontrada através da tabela de propriedades;
- é a velocidade do sistema;
- é a aceleração da gravidade;
- é a altura do sistema.
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. A energia cinética depende da velocidade do sistema e a energia potencial depende da altura do sistema . Como podemos calcular esses dois tipos de energia se não conhecemos nem ?
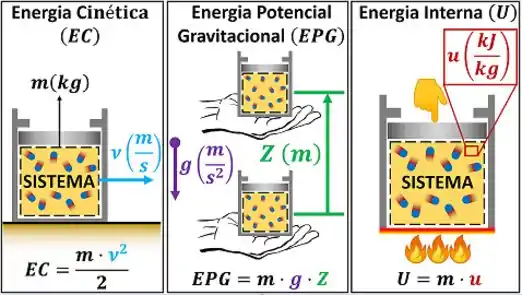
Na verdade, nós não precisamos calcular esses dois tipos de energia! O enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor. Ou seja, a única parte da energia total que varia é a energia interna ! Vamos verificar a variação de energia total do sistema depois dele passar pelo processo.
No entanto:
Por causa disso, as variações de energia cinética e energia potencial gravitacional se anulam e a variação de energia total fica igual à variação de energia interna:
Por outro lado:
Igualando essas duas últimas equações, achamos que:
A energia interna específica é a energia interna específica do líquido saturado a . Já a energia interna específica é a energia interna específica do vapor saturado a .
Isso quer dizer que temos todas as informações para calcular .
Agora vamos substituir todas as informações do enunciado nas equações que descobrimos.
Passo 3
Vamos começar pelos cálculos de através da fórmula abaixo.
Olhando a tabela de saturação, somos capazes de encontrar esses três valores!
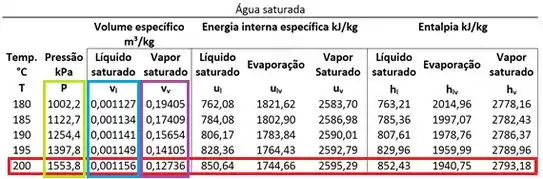
Com esses três valores somos capazes de calcular o trabalho por unidade de massa. Mas atenção! A questão pede que esse valor esteja em quilojoule por quilograma ! Então aqui vai uma dica de como calcular o trabalho na unidade certa.

Para que a unidade do trabalho seja quilojoule , a pressão deve estar em quilopascal e o volume específico em metro cúbico por quilograma !
Para que a unidade do trabalho seja o joule , a pressão deve estar em pascal e o volume específico em metro cúbico por quilograma !
Vamos deixar o cálculo de para o próximo passo!
Passo 4
é calculado pela equação abaixo.
Olhando a tabela de saturação, somos capazes de encontrar os valores de energia interna específica!
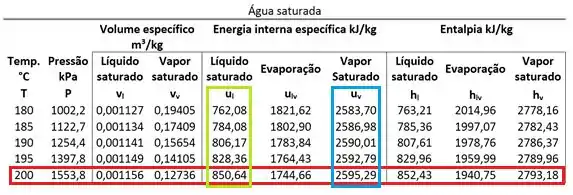
Substituindo esses números na equação de cima, achamos:
Pronto! Calculamos a transferência de calor e o trabalho realizado durante esse processo de condensação!