Um conjunto cilindro-pistão, que apresenta esbarro, contém de água. Inicialmente, o volume e a pressão na água são iguais a e . Quando o pistão encosta no esbarro, o volume da câmara se torna igual a . Transfere-se calor ao sistema até que o pistão toque o esbarro. Determine o calor transferido nesse processo.
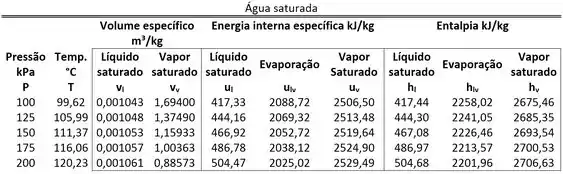
Passo 1
O exercício fala sobre de água que passa por um processo de aquecimento. Conforme a água vai sendo aquecida, o seu volume vai aumentando. Ou seja, conforme a água vai ganhando energia por calor, o pistão vai levantando lentamente. Quando o pistão toca em um obstáculo chamado de esbarro, o aquecimento para e a água fica com de volume.
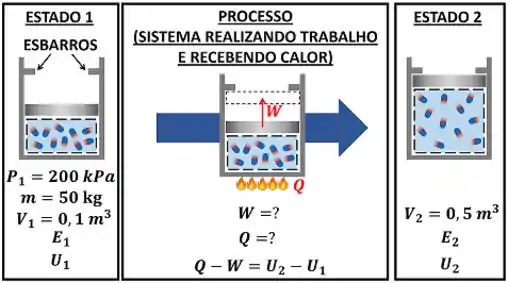
A água inicia o processo no estado 1 com de volume e e termina o processo no estado 2 com de volume e os mesmos de massa. Como nós sabemos os volumes e as massas dos estados 1 e 2, nós já podemos calcular os valores dos volumes específicos da água para os estados 1 e 2!
Além disso, como a água aumenta de volume, a sua fronteira se move. Isso quer dizer que a água realiza trabalho de movimento de fronteira sobre a sua vizinhança. Em outras palavras, enquanto a água ganha energia por calor, ela perde energia por trabalho. E não é qualquer tipo de trabalho! É um trabalho de movimento de fronteira .
Mas como podemos resolver essa integral para calcular o trabalho? Descobrindo uma informação que está escondida no enunciado! Como a água está apoiando o mesmo pistão durante todo o processo, ela está sendo comprimida pelo mesmo peso durante todo o processo. Issosignifica que a pressão sobre ela não muda. Dizendo isso de outro jeito:
O enunciado diz quanto vale a pressão .
Substituindo essa informação na fórmula de trabalho ela muda para:
Saber isso é muito importante! Para calcular a quantidade de calor que a água ganha, nós vamos ter que usar a primeira lei da termodinâmica! Para usar a primeira lei, nós temos que saber quanto vale o trabalho.
Vemos pela equação, que temos que conhecer o trabalho! Mas além disso, também precisamos saber quanto valem as energias internas específicas da água ( e ). Para saber quanto valem as energia internas específicas, nós temos que determinar o estado 1 e o estado 2. Para determinar um estado, nós precisamos conhecer duas propriedades intensivas!

Nós sabemos a pressão do estado 1 e o volume específico do estado 1 . Como conhecemos duas propriedades intensivas desse estado, ele está determinado. O mesmo ocorre com o estado 2. Nós sabemos a pressão do estado 2 e o volume específico do estado 2 ! Isso quer dizer que para achar ( e ) só falta usar a tabela de propriedades!

Mas para usar a tabela de propriedades, nós temos que saber qual é a fase da água primeiro! É isso que aprenderemos a fazer no próximo passo.
Passo 2
Para saber quanto valem e , precisamos descobrir qual é a fase da água nos estados 1 e 2! Para conseguir descobrir, precisamos comparar os volumes específicos da água ( e ) com os volumes específicos informados pela tabela para de pressão.
Onde:
- é o volume específico do líquido saturado a ;
- é o volume específico do vapor saturado a .

Se volume específico for maior que volume específico do vapor saturado a , então a água é um vapor superaquecido no estado 2.
Da mesma forma, se volume específico for maior que volume específico do vapor saturado a , então a água é um vapor superaquecido no estado 1.
Se for menor que volume específico do líquido saturado a , a água é um líquido comprimido no estado 2.
Se for menor que volume específico do líquido saturado a , a água é um líquido comprimido no estado 1.
Por fim, se o valor de estiver entre e , a água está saturada no estado 2.
Por fim, se o valor de estiver entre e , a água está saturada no estado 1.
Se a água for saturada, descobrimos sua energia interna específica olhando para a tabela de saturação. Se a água for vapor superaquecido, descobrimos sua energia interna específica olhando para a tabela de vapor superaquecido. Se a água for líquido comprimido, descobrimos sua energia interna específica olhando para a tabela de líquido comprimido.

Se a água for uma mistura saturada no estado 2, a fórmula de energia interna específica é:
onde:
- é a energia interna específica da parte líquida da mistura a . Ela é o da tabela de saturação para de pressão;
- é a energia interna específica do vapor da mistura a . Ela é o da tabela de saturação para de pressão.
- é o título da mistura do estado 2.
A equação para calcular , caso a água do estado 1 seja saturada, é muito parecida!
Onde é o título da água do estado 1.
Podemos calcular e com as equações abaixo.
Com isso acabamos tudo o que precisávamos entender para calcular o calor trocado . Vamos começar as contas na etapa seguinte!
Passo 3
Começando as contas, encontrando os volumes específicos e .
Para comparar esses valores de volume específico e descobrir a fase da água, precisamos conhecer e . Eles são obtidos através da tabela de saturação da água para a pressão de .
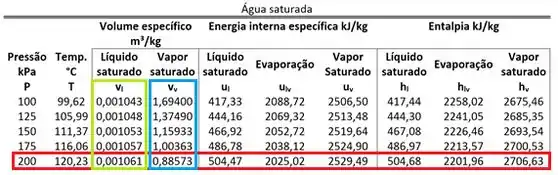
Como os dois volumes específicos e estão entre e , a água está saturada no estado 1 e no estado 2. Ou seja, para achar as energias internas específicas e , nós temos que achar os títulos e .
Para calcular e temos que achar e na tabela de saturação. Isso será feito na próxima etapa!
Passo 4
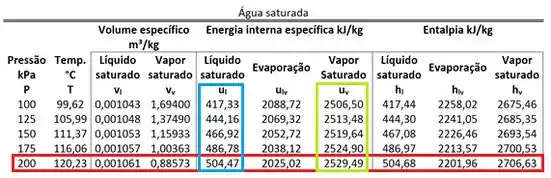
Substituindo esses valores nas equações, encontramos:
Para usar a equação da primeira lei só falta achar o trabalho ! Essa tarefa vai ficar pro passo seguinte!
Passo 5
Sabendo disso, podemos enfim substituir os valores na equação da primeira lei.
Esse é o resultado final!