Um sistema fechado passa por um processo em que não há mudança na energia interna. Durante esse processo, o sistema produz de trabalho. Calcule a transferência de calor para esse processo.
Passo 1
O enunciado fala sobre um sistema fechado que passa por um processo. Nesse processo, o sistema realiza de trabalho e troca calor.
Ou seja, ele troca energia por trabalho e troca de energia por calor.
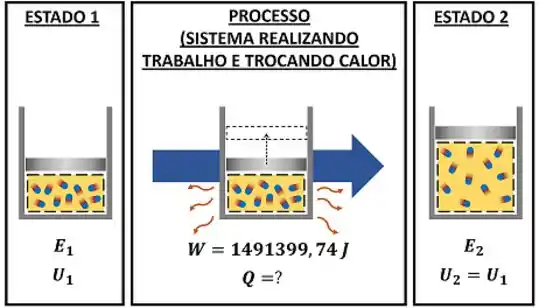
No entanto, mesmo trocando energia de duas formas, sua energia interna não muda! Isso quer dizer que a energia interna no fim do processo e a energia interna no início do processo são iguais.
Sabendo disso, o enunciado quer saber quanta energia foi trocada por calor. Mas como a gente pode calcular a quantidade de energia que o sistema trocou por calor com o ambiente se a gente só sabe a variação de energia interna do sistema? Através da primeira lei da termodinâmica!
A equação dessa lei está escrita acima. Ela diz que o sistema não pode criar nem destruir energia. Isso significa que a variação de energia total do sistema é igual a quantidade d energia que ele troca por calor e trabalho . Mas como a gente pode calcular a variação de energia total , se a gente só conhece a variação de energia interna ?

Isso é o que responderemos no próximo passo!
Passo 2
A primeira etapa para a gente saber como calcular a variação de é olhar para a equação de energia total.
onde:
- é a massa do sistema;
- é a energia interna específica. Ela é encontrada através da tabela de propriedades;
- é a velocidade do sistema;
- é a aceleração da gravidade;
- é a altura do sistema.
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. A energia cinética depende da velocidade do sistema e a energia potencial depende da altura do sistema . Como podemos calcular esses dois tipos de energia se não conhecemos nem ?
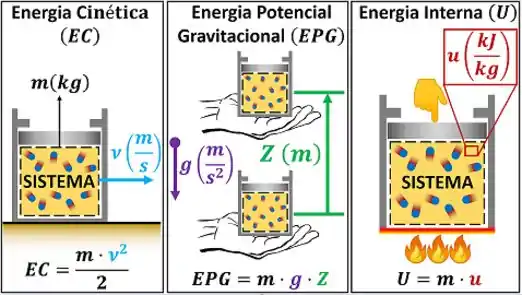
Na verdade, nós não precisamos calcular esses dois tipos de energia! O enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor. Ou seja, a única parte da energia total que varia é a energia interna ! Vamos verificar a variação de energia total do sistema depois dele passar pelo processo.
No entanto:
Por causa disso, as variações de energia cinética e energia potencial gravitacional se anulam e a variação de energia total fica igual à variação de energia interna:
Por outro lado:
Igualando essas duas últimas equações, achamos que:
Como temos e podemos, enfim, calcular a quantidade de energia trocada por calor .
Passo 3
Substituindo os valores do enunciado na última equação, achamos .