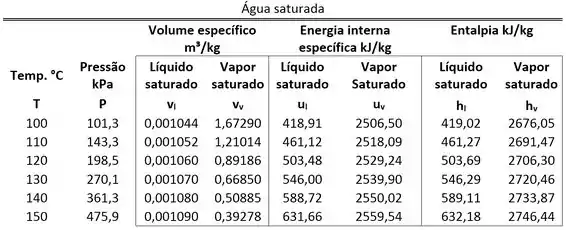
Um sistema fechado, como mostra a Figura abaixo, contém de água líquida saturada a . Ele opera adiabaticamente. Primeiro, ele realiza de energia por trabalho de fronteira. Em seguida, um agitador aplica trabalho ao dispositivo para aumentar a energia interna do fluido em . Calcule a energia interna específica final desse sistema. Use a tabela de propriedades abaixo.
Passo 1
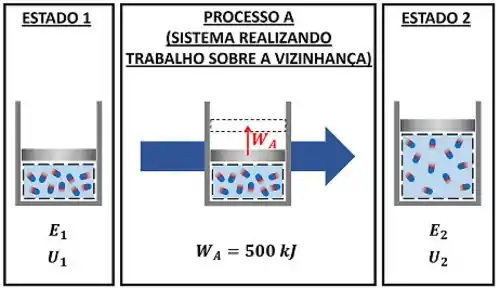
O enunciado fala sobre um sistema fechado que passa por dois processos. No primeiro processo (processo A), o sistema realiza de trabalho sobre a vizinhança. Ou seja, o sistema perde de energia por trabalho de movimento de fronteira e vai do estado 1 ao estado 2. Por causa disso:
A questão também diz que o sistema opera adiabaticamente. Isso significa que ele não troca calor em nenhum dos dois processos.
Como a energia não pode ser criada nem destruída, a variação de energia do sistema durante o processo é igual a energia que o sistema recebe ou perde. Isso é mostrado pela primeira lei da termodinâmica para sistemas fechados.
Com essa equação, nós conseguimos descobrir a energia total do sistema , depois que ele passa pelo processo A.
No segundo processo (processo B), o sistema recebe de energia por trabalho através de um agitador.
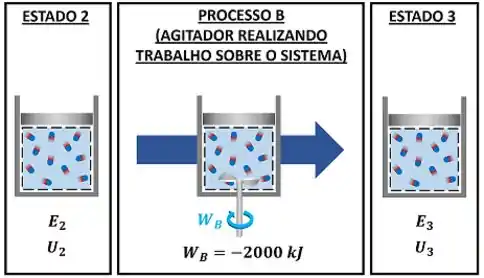
Esse trabalho é negativo, porque pela regra que criamos, quando o sistema realiza trabalho, o trabalho é positivo. Já quando o sistema sofre trabalho, o trabalho é negativo.
A primeira lei para o processo B pode ser escrita como:
Dessa forma, a gente consegue descobrir a energia total do sistema no estado 3 .
No entanto, o exercício quer saber o valor da energia interna específica final da água, depois que ela passa por esses dois processos.
Mas como a gente pode descobrir o valor a energia interna especifica , se nós só sabemos calcular o valor da energia total ? Veremos isso no próximo passo!
Passo 2
A primeira etapa para a gente saber como calcular é olhar para a equação de energia total.
onde:
- é a massa do sistema;
- é a velocidade do sistema;
- é a aceleração da gravidade;
- é a altura do sistema;
- é a energia interna específica do sistema.
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. A energia cinética depende da velocidade do sistema e a energia potencial depende da altura do sistema . Como podemos calcular esses dois tipos de energia se não conhecemos nem ?
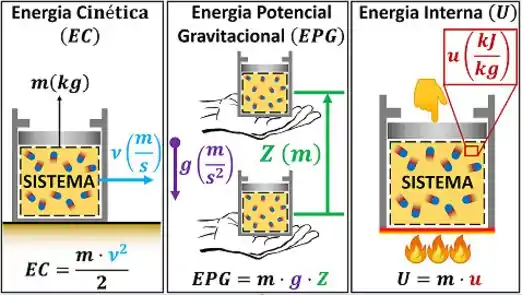
Na verdade, nós não precisamos calcular esses dois tipos de energia! O enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor. Ou seja, a única parte da energia total que varia é a energia interna ! Vamos verificar a variação de energia total do sistema depois dele passar pelo processo A.
No entanto:
Por causa disso, as variações de energia cinética e energia potencial gravitacional se anulam e a variação de energia total fica igual à variação de energia interna:
A mesma coisa acontece para o processo B:
Como a variação de energia total é igual à soma das duas variações de energia, encontramos a seguinte equação:
Por outro lado, a variação de energia total é igual à energia trocado entre o sistema e a sua vizinhança durante esses dois processos.
Igualando as duas equações que desenvolvemos, achamos que:
sendo que o enunciado diz que:
Além disso, como a água é, inicialmente, um líquido saturado a , sua energia interna específica pode ser obtida na tabela de saturação. Ela é igual à para de temperatura.
Como temos todos esses valores, podemos, enfim, calcular a energia interna específica .
Passo 3
O primeiro passo para calcular a energia interna específica é achar na tabela de saturação.
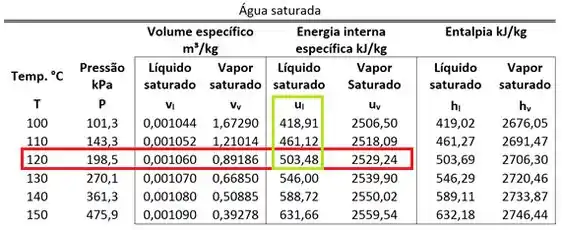
Substituindo os valores do enunciado na última equação, achamos .
Esse é o resultado final!