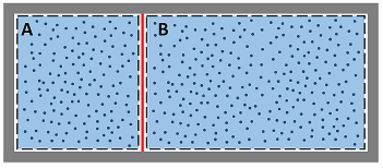
A figura abaixo mostra um tanque que está dividido em duas regiões por meio de uma membrana. A região A apresenta e contém água a e com . A região B contém de água a e . A membrana é, então, rompida e espera-se que seja estabelecido o equilíbrio. Sabendo que a temperatura final do processo é , determine a transferência de calor que ocorre durante o processo.
Passo 1
O enunciado fala sobre um tanque cheio de água que passa por um processo de troca de calor com o ambiente. Antes de trocar calor (estado 1), o tanque está dividido em duas partes: parte A e parte B. Assim que a membrana que separa as duas partes é rompida, a troca de calor começa. A água que estava na parte A se mistura com a água que estava na parte B (estado 2).
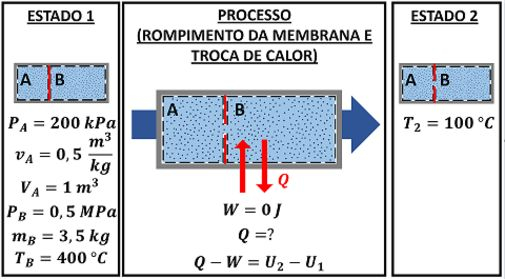
A questão quer saber quanto vale essa troca de calor . Para calcular isso, precisamos usar a primeira lei da termodinâmica.
Precisamos de , e para achar . Vamos começar pelo trabalho !
Quando a membrana se rompe, a água que estava na parte A se expande para a parte B e a água que estava na parte B se expande para a parte A. Essas duas expansões são consideradas trabalho de movimento de fronteira?

Essa expansão não é trabalho! Ela é expansão não resistida! Mas se a água que estava presa em uma das partes aumenta o seu volume, por que não consideramos que ela realiza trabalho?

Porque para ser trabalho, ela deveria empurrar a outra parte de água com uma força! Mas na verdade ela se mistura com a outra, ao invés de empurrar a outra parte.
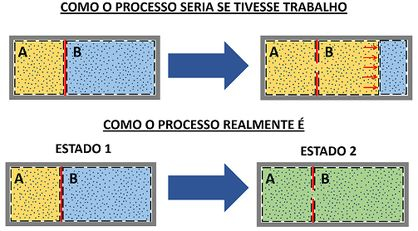
Isso quer dizer que o processo de expansão não tem trabalho.
Agora, para calcular só falta encontrar as energias internas e .
O estado 1 da água está dividido em parte A e parte B. Isso significa que a energia interna total desse estado é a soma da energia interna de cada parte ( e ).
Para calcular a energia interna de cada parte, devemos nos lembrar da equação de energia interna.
onde:
- é a energia interna específica da parte A no estado 1;
- é a energia interna específica da parte B no estado 1;
- é a massa de água da parte A no estado 1;
- é a massa de água da parte B no estado 1.
Entenderemos como calcular cada uma dessas quatro variáveis na próxima etapa.
Passo 2
Para calcular , precisamos reorganizar a equação de volume específico .
O enunciado já fornece diretamente e .
Como o enunciado informa a pressão e o volume específico da parte A no estado 1, o estado da parte A já está definido. Isso quer dizer que para achar , só temos que descobrir a fase da parte A e depois pegar na tabela de propriedades.

Para conseguir descobrir a fase, precisamos comparar o volume específico da água com os volumes específicos informados pela tabela para de pressão.
Onde:
- é o volume específico do líquido saturado a de pressão;
- é o volume específico do vapor saturado a de pressão.
- é a energia interna específica da parte líquida da mistura a de pressão. Ela é o da tabela de saturação para de pressão;
- é a energia interna específica do vapor da mistura a de pressão. Ela é o da tabela de saturação para de pressão.
- é o volume específico do líquido saturado a de temperatura;
- é o volume específico do vapor saturado a de temperatura.
- é a energia interna específica da parte líquida da mistura a de temperatura. Ela é o da tabela de saturação para de temperatura;
- é a energia interna específica do vapor da mistura a de temperatura. Ela é o da tabela de saturação para de temperatura.

Se volume específico for maior que volume específico do vapor saturado a de pressão , então a água é um vapor superaquecido.
Se for menor que volume específico do líquido saturado a de pressão , a água é um líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Se a água da parte A estiver saturada, vamos precisar conhecer o seu título para calcular .
Depois, usamos esse valor na fórmula de .
onde:
O enunciado informa diretamente a temperatura e a pressão da parte B.
Com essas duas propriedades intensivas, o estado 1 da parte B está definido! Isso significa que para encontrar só precisamos descobrir sua fase e depois achar a energia interna específica na tabela.

Para descobrir a fase da parte B, comparamos a temperatura com a temperatura de saturação da parte B para de pressão!
Se for maior que , então a água da parte B é vapor superaquecido.
Se for menor que , então a água da parte B é líquido comprimido.
Se for igual a , então a água da parte B está saturada.
Se a parte B for saturada, pegamos a energia interna específica pela tabela de saturação. Se a parte B for vapor superaquecido, pegamos a energia interna específica pela tabela de vapor superaquecido. Se a parte B for líquido comprimido, pegamos a energia interna específica pela tabela de líquido comprimido.

A massa da parte B é informada diretamente pelo enunciado.
No próximo passo, vamos aprender a calcular a energia interna para conseguir achar .
Passo 3
A equação da energia interna final da água é:
Como a massa de água no tanque não muda com a troca de calor, o valor de é igual à soma das massas da parte A e da parte B .
A primeira etapa para achar é definir o estado 2. Para isso, precisamos do valor de duas propriedades intensivas desse estado. O enunciado já informa a temperatura desse estado .
Resta saber o valor de outra propriedade intensiva. Para conseguir isso, temos que lembrar que o volume total do tanque não muda. Ou seja, o volume do tanque depois de troca de calor é igual a soma dos volumes das partes A e B antes da troca de calor.
O volume da parte B é calculado, reorganizando a equação do volume específico .
O volume específico é obtido pela tabela de propriedades.
A partir desse valor de volume , podemos calcular a propriedade intensiva e definir o estado 2.
A etapa final para achar é descobrir a fase da água no estado 2.
Para conseguir descobrir a fase, precisamos comparar o volume específico da água com os volumes específicos informados pela tabela para de temperatura.
Onde:

Se volume específico for maior que volume específico do vapor saturado a de temperatura , então a água é um vapor superaquecido.
Se for menor que volume específico do líquido saturado a de temperatura , a água é um líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Se a água do estado 2 estiver saturada, vamos precisar conhecer o seu título para calcular .
Depois, usamos esse valor na fórmula de .
onde:
Com todas essas informações, podemos calcular através da primeira lei da termodinâmica. Mas vamos deixar essa etapa para o passo seguinte!
Passo 3
Iniciamos os cálculos descobrindo quanto vale a massa de água que está inicialmente na parte A.
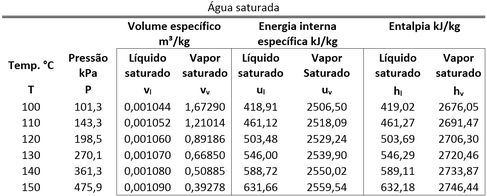
Para achar a fase da parte A, temos que comparar com e . Esses dois volumes específicos são encontrados na tabela de saturação da água.
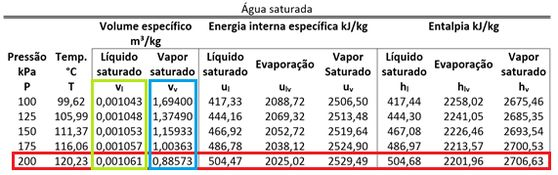
Como é , seu valor está entre e . Isso quer dizer que a água da parte A está saturada. Sabendo disso, temos que descobrir o título para calcular .
Também precisamos dos valores de e para cacular . Essas duas energias intenas específicas são encontradas na tabela de saturação da água.
Substituindo esses valores na fórmula de , achamos que:
Já que temos a massa e a energia interna específica da parte A, podemos achar sua energia interna .
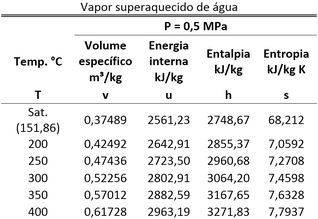
Para achar a energia interna do estado 1, só falta saber quanto vale a energia interna específica da parte B. Para isso, descobrimos a fase da parte B, comparando a temperatura com a temperatura de saturação da parte B para de pressão. Essa temperatura de saturação é obtida pela tabela do vapor superaquecido.
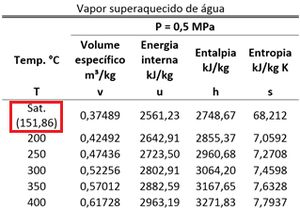
Como a temperatura da parte B é maior que a temperatura de saturação , a água da parte B é um vapor superaquecido. Isso significa que a energia interna específica está na tabela de vapor superaquecido.
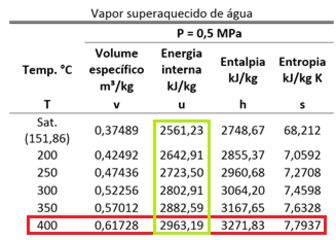
Agora podemos calcular a energia interna da parte B .
A energia interna total da água no estado 1 vale:
O cálculo de ficará para o passo a seguir.
Passo 4
A massa do estado 2 vale:
Já o volume do estado 2 precisa do valor da parte B para ser encontrado.
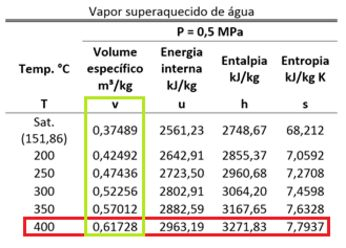
Sabendo disso:
Com a massa e o volume do estado 2, somos capazes de achar o volume específico desse estado.
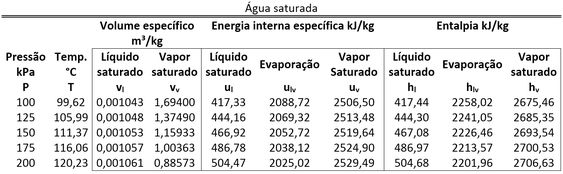
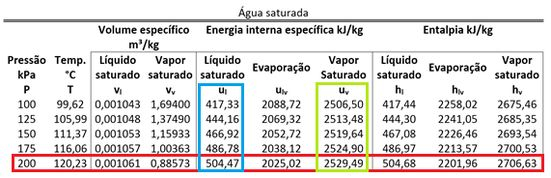
Com esse valor, achamos a fase da água no estado 2. Para descobrir isso, pegamos e na tabela de saturação.
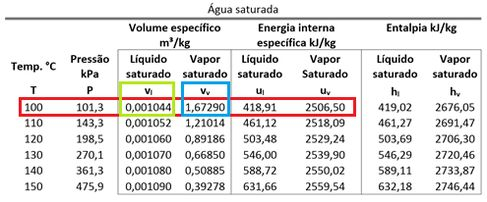
Como é , seu valor está entre e . Isso quer dizer que a água no estado 2 está saturada. Sabendo disso, temos que descobrir o título para calcular .
Também precisamos dos valores de e para cacular . Essas duas energias intenas específicas são encontradas na tabela de saturação da água.
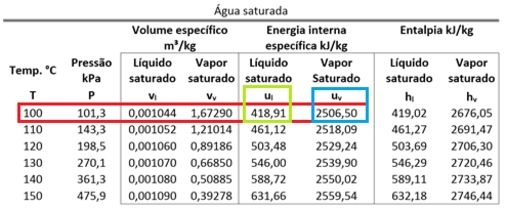
Substituindo esses valores na fórmula de , achamos que:
A energia interna do estado 2 é:
Com esse valor nós finalmente somos capazes de calcular o calor trocado no passo seguinte!
Passo 5
Substituindo todos os valores que encontramos na primeira lei da termodinâmica, achamos:
Esse é o resultado final!