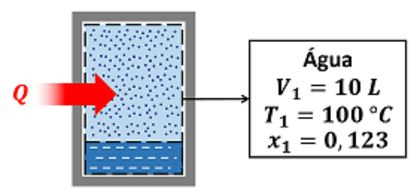
Um vaso rígido de inicialmente contém uma mistura de líquido e vapor de água a com título de . A mistura é então aquecida até que a sua temperatura seja de . Calcule a transferência de calor necessária para este processo.
Passo 1
O exercício diz que um sistema passa por um processo de aquecimento. O sistema é formado inicialmente por uma mistura de líquido e vapor de água a com título de . Depois de ser aquecido, atinge de temperatura (estado 2). A fase do estado final (estado 2) não foi informada. A figura abaixo mostra o sistema antes e depois do processo.
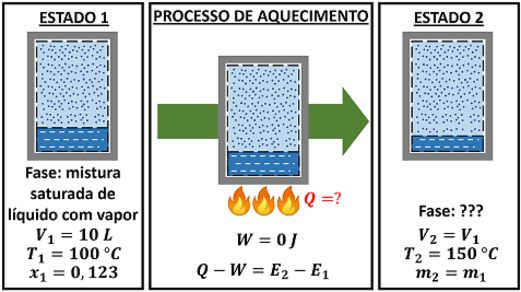
A imagem mostra que o calor pode ser calculado através da primeira lei da termodinâmica.
Mas como podemos calcular se não conhecemos quanto vale o trabalho ?
Na verdade o enunciado fala quanto vale o trabalho. No entanto é um tipo de informação que está escondida nele. Quando ele diz que a água está dentro de um vaso rígido, ele quer dizer que a fronteira do sistema não se move! Ou seja, o volume do sistema não muda!
Um vaso rígido é a mesma coisa que um tanque rígido. Os dois são usados para guardar uma substância! Além disso, nenhum dos dois muda de forma ou varia o seu volume!
Por causa disso, o trabalho de movimento de fronteira vale zero!
Mas e a variação da energia total ? Como podemos calcular?
Nós vemos que a energia total é formada por três tipos de energia: energia cinética, energia potencial gravitacional e energia interna. No entanto, o enunciado não fala que o sistema varia de velocidade ou de altura. Isso significa que essas duas variáveis não mudam de valor.
Ou seja, a única parte da energia total que varia é a energia interna !
onde:
- é a energia interna específica da água a ;
- é a energia interna específica da mistura de líquido com vapor a ;
- é a massa do sistema no início;
- é a massa do sistema no fim do processo de aquecimento.
- é a energia interna específica da parte líquida da mistura a . Ela é o da tabela de saturação para de temperatura;
- é a energia interna específica do vapor da mistura a . Ela é o da tabela de saturação para de temperatura.
- é o título da mistura do estado 1. Ele vale segundo o enunciado
- é o volume específico do líquido saturado contido na mistura. Ele está a segundo o enunciado;
- é o volume específico do vapor saturado contido na mistura. Ele está a segundo o enunciado.
- é o volume específico do líquido saturado a ;
- é o volume específico do vapor saturado a .
- é a energia interna específica da parte líquida da mistura a . Ela é o da tabela de saturação para de temperatura;
- é a energia interna específica do vapor da mistura a . Ela é o da tabela de saturação para de temperatura.
- é o título da mistura do estado 2.
Como o estado 1 é uma mistura de líquido com vapor, sua energia interna é calculada pela fórmula abaixo:
onde:
O estado 1 já está definido! Mas como nós podemos definir o estado 2, se nós temos apenas sua temperatura ?
Descobriremos isso no próximo passo!
Passo 2
Precisamos conhecer mais uma propriedade intensiva do estado 2 para fixarmos este estado e descobrirmos as suas propriedades intensivas restantes. Fazemos isso levando em conta outra informação escondida no enunciado. Como o problema não diz que água entra ou sai do vaso, nós deduzimos que a massa de água permanece igual durante todo o aquecimento.
Como o volume e a massa de água permanecem iguais durante todo o processo, seu volume específico também permanece igual:
Ou seja, dessa forma descobrimos mais uma propriedade intensiva do estado 2 e conseguimos fixar esse estado.
Mas como encontramos o volume específico , se nós não sabemos quanto vale a massa ?

Através da tabela de saturação! Como o estado 1 é uma mistura saturada de líquido e vapor de Refrigerante 22, o volume específico é dado pela fórmula abaixo.
onde:
Com esse valor, podemos reorganizar a equação de volume específico e encontrar a massa de água.
Agora só falta encontrar ! O próximo passo vai mostrar como fazer isso!
Passo 3
Para saber quanto vale , precisamos descobrir qual é a fase da água nesse estado! Para conseguir descobrir, precisamos comparar o volume específico da água com os volumes específicos informados pela tabela para de temperatura.
Onde:

Se volume específico for maior que volume específico do vapor saturado a , então a água é um vapor superaquecido.
Se for menor que volume específico do líquido saturado a , a água é um líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Se a água for uma mistura saturada, a fórmula de energia interna específica é:
onde:
Podemos calcular com a equação abaixo.
Com isso acabamos tudo o que precisávamos entender para calcular o calor trocado . Vamos começar as contas na etapa seguinte!
Passo 2
O primeiro passo para resolver essa questão é descobrir quanto vale pela equação abaixo.
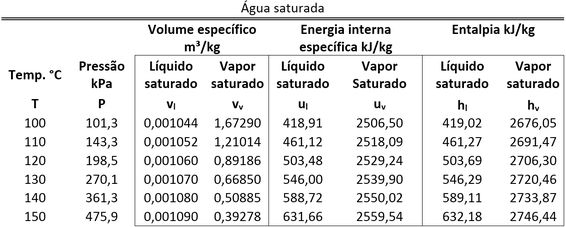
e podem ser obtidos através da tabela de saturação da água para a temperatura de .
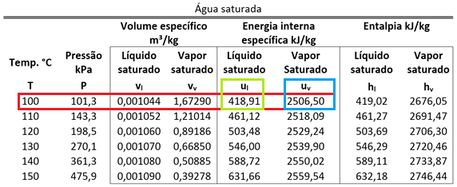
O segundo passo para resolver esse exercício é encontrar o volume específico da água antes do aquecimento .
e podem ser obtidos através da tabela de saturação da água para a temperatura de .
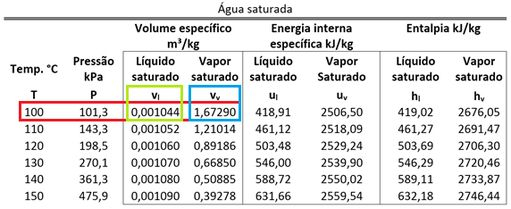
Com esse valor conseguimos calcular a massa de água contida no vaso rígido.
Agora só falta ! Mas vamos deixar a determinação de para o outro passo.
Passo 3
Para saber o valor de , precisamos encontrar e para descobrir a fase da água no estado 2. Eles estão na tabela de saturação!
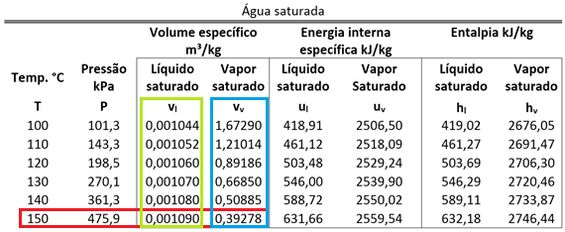
O volume específico é igual ao volume específico .
Como está entre e , a água do estado 2 está saturada! Para achar o seu título , devemos usar a fórmula abaixo.
Com esse valor, só falta achar e para calcular pela equação abaixo.
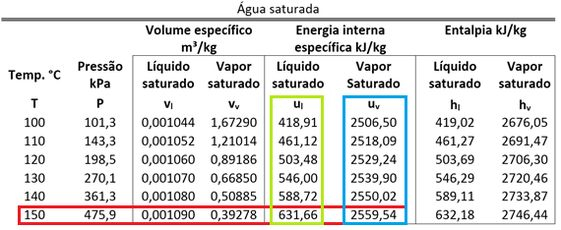
Com isso, nós achamos a variação de energia total da água por causa do aquecimento.
Substituindo todas as incógnitas que nós entramos na fórmula de cálculo de , podemos achar esse resultado final!
Enfim, chegamos no resultado final!