Considere as seguintes afirmações:
- A intensidade da radiação eletromagnética emitida por um dipolo elétrico, na aproximação pontual, é esfericamente simétrica e decai com o inverso do quadrado da distância do dipolo.
- Os campos elétrico e magnético de uma onda eletromagnética plana e monocromática são sempre perpendiculares entre si.
- O campo magnético de uma onda estacionária, dentro de uma cavidade metálica, não é identicamente nulo nas paredes da cavidade.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Apenas é verdadeira.
- Apenas é verdadeira
- Apenas é verdadeira.
- Todas as afirmativas são verdadeiras.
- Nenhuma afirmativa é verdadeira.
Passo 1
“A intensidade da radiação eletromagnética emitida por um dipolo elétrico, na aproximação pontual, é esfericamente simétrica e decai com o inverso do quadrado da distância do dipolo.”
FALSO
Uma outra forma de dizer que a “intensidade da radiação é esfericamente simétrica” é dizer que ela depende apenas da distância entre o dipolo e o ponto no espaço.
No caso da radiação emitida pelo dipolo oscilante, a intensidade também depende do ângulo entre o eixo do dipolo e a distância do ponto ao dipolo, da seguinte forma:
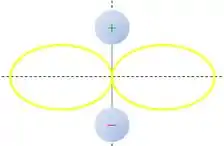
Passo 2
“Os campos elétrico e magnético de uma onda eletromagnética plana e monocromática são sempre perpendiculares entre si.”
VERDADEIRO
A primeira afirmação é verdadeira: SEMPRE, em uma onda eletromagnética plana e monocromática, (campo elétrico) e (campo magnético) serão perpendiculares entre si.
O motivo disso são as leis de Faraday-Lenz e Ampère-Maxwell, que restringem o formato das oscilações elétrica e magnética.
Não é necessário o próximo desenvolvimento, mas pra quem por algum motivo quiser saber como faz isso que eu falei.
Colocamos a forma senoidal dos campos (onde coloquei a mais geral possível):
Na lei de Ampère-Maxwell (no vácuo) ou na Lei de Faraday:
Usando a lei de Ampère-Maxwell:
Essa última expressão é basicamente um produto vetorial (não, não é fácil ver isso).
O motivo de inverter o produto vetorial é que, antes de eu resolver isso aqui, eu passei 2 horas confuso, e aí percebi que valeria a pena fazer isso pra não deixar você 2 horas confuso(a).
Juntando os dois:
Agora, cortando o menos dos dois lados (sinais de menos: confundindo alunos de física desde a babilônia) e sabendo que , temos:
Onde é o vetor unitário de propagação da onda. Pela regra da mão direita, essa igualdade que a gente deduziu implica nisso aqui:
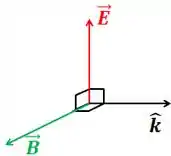
Ou seja, é perpendicular a .
Passo 3
“O campo magnético de uma onda estacionária, dentro de uma cavidade metálica, não é identicamente nulo nas paredes da cavidade.”
VERDADEIRO
Uma cavidade metálica é boa condutora de eletricidade. Isso significa que a sua superfície vai ser o que chamamos uma “equipotencial” (Superfície tal que todos os pontos têm o mesmo potencial elétrico).
O campo elétrico é igual ao negativo do gradiente do potencial.
O que significa que é sempre perpendicular à uma equipotencial, especificamente ele vai ser perpendicular à superfície da cavidade.
Como é sempre perpendicular a em uma onda eletromagnética, então vai ser tangencial à equipotencial.
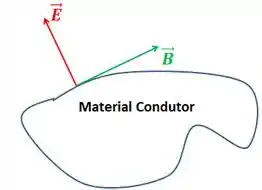
Assim, não necessariamente é nulo. Apenas a componente perpendicular à superfície da cavidade será nula. Por isso, de fato, na parede da cavidade.
Resposta então vai ser a letra , “Apenas e são verdadeiras”.
Resposta
Letra
Apenas e são verdadeiras.