A figura abaixo representa os campos elétrico e magnético de uma onda eletromagnética plana monocromática, no vácuo, na origem do sistema de coordenadas em dois instantes diferentes. Nestes dois momentos . A frequência da onda é e sua velocidade de propagação .
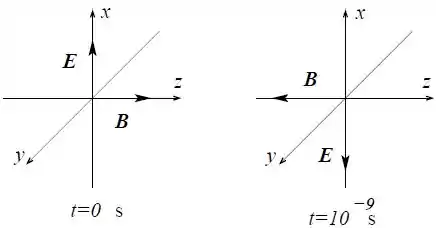
Determine o sentido de propagação da onda. Calcule o comprimento de onda , a frequência angular e o número de onda .
Escreva a expressão completa do vetor campo elétrico indicando a dependência nas coordenadas e no tempo.
Escreva a expressão do campo magnético associado ao campo elétrico dado.
Passo 1
Determine o sentido de propagação da onda. Calcule o comprimento de onda , a frequência angular e o número de onda .
Para determinar o sentido de propagação da onda, é importante você lembrar que o produto vetorial entre e aponta na mesma direção e sentido de propagação da onda.
Em , aponta no sentido vetor e o vetor aponta no sentido , logo:
Assim, a onda se propaga na mesma direção e sentido do vetor .
Passo 2
Aqui precisamos lembrar de algumas fórmulas que, vira e mexe, aparecem na nossa vida:
Bom, acho que com isso aqui a gente começa a se virar.
O problema nos deu e , então podemos começar calculando , usando a primeira fórmula.
Então vamos aproveitar o embalo e calcular o número de onda
Pra fechar, vamos calcular a frequência angular .
Passo 3
Escreva a expressão completa do vetor campo elétrico indicando a dependência nas coordenadas e no tempo.
Os dois gráficos mostram que o campo elétrico se propaga na direção .
Logo, a expressão do vetor campo elétrico vai ter essa cara:
Obs.: O sinal aqui é positivo porque a onda se propaga no sentido do vetor . Se ela se propagasse no sentido do vetor , por exemplo, o sinal seria negativo . Ou seja, o sinal é sempre do contra!
Ok, dessa expressão, as únicas coisas que não sabemos são os valores de e de , então vamos utilizar as condições de contorno pra encontrar esses valores, ok?
- ;
- ;
Ok! Agora vamos trabalhar com esses caras!
Passo 4
Dividindo as duas equações, teremos:
Opa! Substituindo esse cara em uma das situações, teremos:
Finalmente, o campo elétrico será dado por:
Acabou, mas se quiser ajeitar esse cara pra ficar melhor, podemos reescrevê-lo assim:
Passo 5
Escreva a expressão do campo magnético associado ao campo elétrico dado.
Os dois gráficos mostram que o campo magnético se propaga na direção .
Mas como saber se o campo magnético está no sentido de ou de ??
Já sabemos que o campo elétrico está no sentido de e que a onda se propaga no sentido de . Então agora é só testar:
Sendo assim, o campo magnético se propaga no sentido de .
Logo, a expressão do vetor campo elétrico vai ter essa cara:
Já temos todos os dados, exceto . Mas aqui, basta lembrar que:
Finalmente:
Resposta
A onda se propaga na mesma direção e sentido do vetor .