Um aquecedor por radiação cilíndrico apresenta comprimento e diâmetro igual a e . A potência dissipada no aquecedor é . Admitindo que a emissividade da superfície do aquecedor seja igual a e desprezando a radiação que incide no aquecedor, determine a temperatura superficial deste aquecedor.
Passo 1
Fala, gente! Partiu fazer um exercício de radiação pra gravar bem a matéria?

Essa questão quer saber quanto vale a temperatura superficial de um aquecedor que emite uma taxa de calor por radiação de . A figura abaixo mostra os dados que temos para calcular .
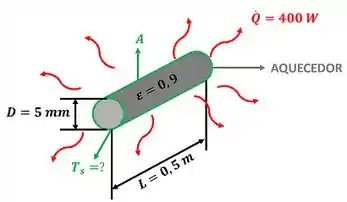
é a emissividade da superfície do aquecedor, é a área da superfície do aquecedor, é o comprimento do aquecedor e é o diâmetro do aquecedor.
Para calcular a temperatura de uma superfície que emite radiação, temos sempre que usar a lei de Stefan-Boltzmann mostrada abaixo.
Reorganizando a equação:
Agora que sabemos de tudo isso, podemos partir pro cálculo de no próximo passo.
Passo 2
Antes de atacar o problema e substituir os valores que temos na fórmula, temos que lembrar de calcular a área em . Pra isso, usamos a fórmula que calcula a área total de um cilindro presente na figura abaixo.
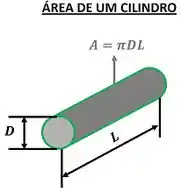
Além disso, precisamos converter a unidade do diâmetro de pra , dividindo por .
Lembrando que a constante de Stefan-Boltzmann vale sempre , podemos substituir os dados na fórmula de e achar logo esse valor. Mas ATENÇÃO! A temperatura calculada a partir da lei de Stefan-Boltzmann está sempr em kelvin . Logo, o resultado que vamos obter será em !
Isso aííííí! Resolvemos o exercício! Mandamos muito!