Um corpo cuja área superficial é , emissividade é e temperatura é é colocado em uma grande câmara de vácuo, cujas paredes estão a . Qual a taxa de radiação emitida pela superfície em ? Qual é a taxa líquida de radiação trocada entre a superfície e as paredes da câmara, em ?
Passo 1
Então, gente, esse é um exercício de radiação que pede duas informações. Primeiro, a questão pede o valor da taxa de calor que um corpo emite por radiação. Depois, ela pede o valor da taxa de calor que o corpo e a câmara trocam por radiação! Essa taxa de calor é igual à taxa que o corpo emite, menos a taxa que ele absorve de radiação da câmara.
A figura abaixo mostra os dados que temos pra calcular .
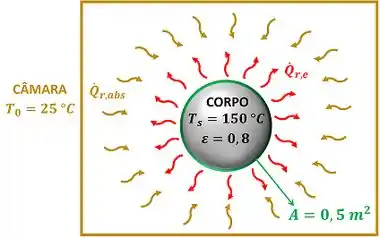
é a área do corpo, é a temperatura da superfície do corpo, é a temperatura da câmara e é a emissividade do corpo.
Pra calcular e , usaremos a lei de Stefan-Boltzmann.
Sabendo de tudo isso, podemos partir pro próximo passo que é calcular .
Passo 2
Como dito, calculamos a taxa de calor emitido por radiação pelo corpo através da lei de Stefan-Boltzmann abaixo.
onde é a constante de Stefan-Boltzmann que vale sempre e é a emissividade da superfície. O enunciado informou que o valor dessa emissividade vale ! Para achar temos que converter a temperatura de pra , somando com .
Substiuindo os dados na fórmula de :
Obaaaa! Já achamos a primeira informação que o enunciado pediu pra gente!
Agora só falta achar pra calcular !
Passo 3
Para calcular a taxa de calor por radiação que o corpo absorve, temos que saber que um corpo com emissividade de absorve das radiações que chegam até ele por todos os lados. Logo, da radiação emitida pela vizinhança a é absorvida pelo corpo.
Substituindo e na equação de :
Uhuuuul! Achamos a segunda informação que o enunciado nos pediu e acabamos a questão!