Uma esfera com de diâmetro cuja superfície é mantida à temperatura de é suspensa no meio de uma sala a . Considerando que o coeficiente de transferência de calor por convecção é de e a emissividade da superfície corresponde , determine a taxa total de transferência de calor da esfera.
Passo 1
Oi, chuchus, pront@s pra essa questão que mistura convecção com radiação?
O enunciado pede para a gente calcular a taxa de calor que a superfície de uma esfera perde de duas formas. Uma parte de , que chamaremos de , é perdida por convecção. Essa parte é calculada com a lei de resfriamento de Newton abaixo.
onde é o coeficiente de transferência de calor por convecção de , é a área da superfície esférica com diâmetro de , é a temperatura da superfície que vale e é a temperatura do ar a .
A outra parte de é perdida por radiação e é calculada abaixo:
Essa fórmula mostra que, pra gente calcular a parcela que a superfície perde por radiação, temos que calcular a quantidade que ela perde por emitir radiação menos a quantidade que ela ganha por absorver radiação das superfícies ao redor! Essas duas taxas são calculadas através da lei de Stefan-Boltzmann. A figura abaixo mostra melhor o problema.
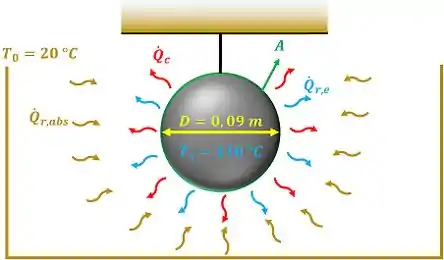
Com essas informações, vamos iniciar as contas no passo seguinte!
Passo 2
Vamos iniciar as contas, calculando a taxa de calor que a superfície perde por convecção.
Fazemos isso, substituindo os dados que temos na fórmula de do passo 1.
No entanto, antes precisamos calcular a área da superfície esférica através da equação abaixo.
Agora sim podemos substituir os dados.
No próximo passo calcularemos !
Passo 3
Pra calcular a parcela de taxa de calor que a superfície perde por radiação, temos que achar a taxa que ela emite por radiação. A equação abaixo calcula esse valor.
onde é a constante de Stefan-Boltzmann que vale sempre e é a emissividade da superfície. O enunciado informou que o valor dessa emissividade vale ! Para achar só falta converter a temperatura de pra , somando com .
Substiuindo os dados na fórmula de :
Agora só falta achar pra calcular e !
Passo 4
Para calcular a taxa de calor por radiação que o corpo esférico absorve, temos que saber que um corpo com emissividade de absorve das radiações que chegam até ele por todos os lados. Logo, da radiação emitida pela vizinhança a é absorvida pela esfera.
Substituindo e na equação de :
Agora é só somar e pra achar .
Acabooooou! Encontramos o resultado que o enunciado pediu!