A superfície de uma tora de madeira, que está localizada em uma fornalha, é . Admitindo que a emissividade da superfície da tora seja igual a (corpo negro perfeito), determine a taxa de emissão de energia por radiação na superfície da tora.
Passo 1
Fala, gente! Partiu fazer um exercício de radiação pra gravar bem a matéria?

Essa questão quer saber quanto vale a taxa de calor emitida por radiação por uma tora dividida pela área da superfície da tora. Em outras palavras, a questão quer saber quanto vale . A figura abaixo mostra os dados que temos para calcular esse valor.
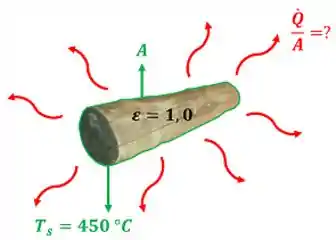
é a emissividade da superfície da tora de madeira e é a temperatura da superfície da tora de madeira.
Para calcular a taxa de calor emitida pela radiação de uma superfície, temos sempre que usar a lei de Stefan-Boltzmann mostrada abaixo.
Agora que sabemos de tudo isso, podemos partir pro cálculo de no próximo passo.
Passo 2
Antes de atacar o problema e substituir os valores que temos na fórmula, temos que lembrar de uma regra muito importante que precisamos seguir pra utilizar a lei de Stefan-Boltzmann corretamente! Essa regra diz que a temperatura tem SEMPRE que estar em kelvin pra usarmos essa equação. Pra converter de pra , precisamos somar à temperatura!
Além disso, precisamos lembrar que a constante de Stefan-Boltzmann vale SEMPRE .
Agora sim podemos substituir os valores na equação que temos e achar .
Uhuuuul! Achamos o resultado da questão! Arrasamos!