A temperatura e a emissividade da superfície externa de uma casa são iguais a e . A temperatura e a emissividade média do ambiente que circunda a casa são igual a e . Determine a taxa de emissão de radiação por unidade de área na superfície externa da casa e no ambiente.
Passo 1
Oi, gente! Como vão? Estudando radiação pra tirar 10 na prova?
Essa questão de radiação pede que a gente calcule dois termos. Ela quer que a gente ache o valor da taxa de calor por unidade de área emitida por radiação por uma casa e pede que a gente ache a taxa de calor por unidade de área emitida por radiação pelo ambiente.
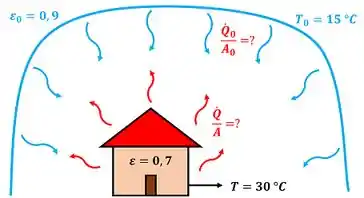
e são a emissividade e temperatura da superfície da casa respectivamente. e são a emissividade e a temperatura do ambiente.
Pra calcular e da radiação, usamos a lei de Stefan Boltzmann. Escrevemos abaixo a lei de Stefan Boltzmann pra casa e pro ambiente.
Com essas duas equações e os dados da figura, já somos capazes de calcular e no próximo passo.
Passo 2
Pra achar e precisamos lembrar que a constante de Stefan-Boltzmann vale sempre . Além disso, temos que lembrar que as temperaturas e tem SEMPRE que estar em kelvin pra usarmos essas equações. Pra converter de pra , precisamos somar às temperaturas! Com isso em mente, vamos achar primeiro.
Opa! Já achamos um dos valores que o enunciado pediu! Agora vamos achar !
Feshoooow! Acabamos com a questão! Já estamos ficando muito craques em radiação! :)