Calcule a integral abaixo utilizando a Regra dos Trapézios Simples
Passo 1
Fala Aíí!! Vamos dar uma olhadinha no gráfico da função no intervalo de 1 até 2? Consegue imaginar o que estamos fazendo?
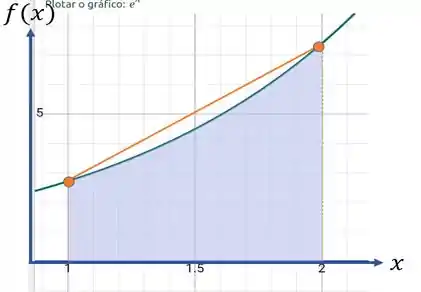
Pensa comigo, nós pegamos dois pontos da função e colocamos uma reta ligando os dois em a e b... conseguiu enxergar a fórmula geométrica do trapézio que aparece quando fazemos isso?

Relembrando um pouquinho: Por definição Integral é a área sob a curva, e nós vamos nos concentrar na área do Trapézio pra solucionar a integral, lembra da fórmula para calcular a Área de um Trapézio?
Diz aí, fórmula da área do trapézio não é beeeeem parecida com a Integral?
No nosso caso a altura () é a distância no intervalo [a,b] no eixo x em que a função está inserida e também o nosso passo já visto anteriormente, o trapézio menor é o e o trapézio maior é o .
Passo 2
Agora a primeira coisa que vamos calcular é o , sabendo que a função exponencial está em um intervalo de .
O próximo passo é substituir os valores na equação da Integral do polinômio:
Logo, a integral utilizando a Regra dos Trapézios Simples vale
Show de bola?!