Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra dos Trapézios

Exercício 61234578910

Enunciado

Empregando-se a Regra dos Trapézios para calcular a integral de x 3 entre 0 e   1 com dois intervalos, tem-se como resposta o valor de:

  1. 0.2750
  2. 0.3000
  3. 0.2500
  4. 0.3225
  5. 0.3125

Passo 1

Vamos lá!! Nesse exercício queremos utilizar a regra trapézio para calcular a integral abaixo

∫ 0 1 x 3 d x

Só que com dois intervalos, ou seja

n = 2

Beleza?!

E agora? Temos que o gráfico da função x 3 no intervalo entre 0 e 1 é:

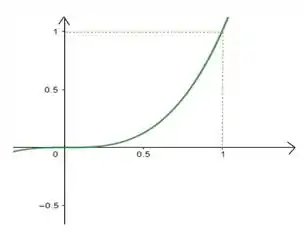
Aqui nosso   h passa a ser:

h =     x n -   x 0 n

Ou seja, os pontos estão igualmente espaçados entre si.

Assim, substituindo os valores, temos

h =   1 - 0 2 = 1 2 = 0.5

Ou seja, a distância entre o x 0 e o x 1 vale 0.5 e, da mesma foram a distância entre x 1 e x 2 vale 0.5 :

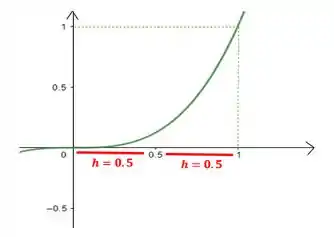
Show de bola?!

Passo 2

Aqui como estamos trabalhando com mais de um intervalo, vamos usar a fórmula da regra do Trapézio repetida:

I T R = h 2 [ f ( x 0 ) + 2 f x 1 + 2 f ( x 2 ) + … + 2 f ( x n - 1 ) + f ( x n ) ]

Nesse exercício temos dois intervalos, ou seja, três pontos

x 0 = 0

x 1 = 0.5

x 2 = 1

Assim, a nossa fórmula ficará com a seguinte carinha

I T R = h 2 [ f ( x 0 ) + 2 f x 1 + + f ( x 2 ) ]

Portanto, substituindo os valores, temos

I T R = 0.5 2 [ f ( 0 ) + 2 f 0.5 + + f ( 1 ) ]

Agora é só fazer as continhas!!

I T R = 0.5 2 [ 0 + 2 0,125 + 1 ]

I T R = 0.3125

Logo, a nossa resposta é a letra E!

Resposta

Letra E!