Os métodos da integração numérica em regra não são exatos. Suponhamos o método de Simpson (trapézios) em sua apresentação mais simples mostrado na figura a seguir.

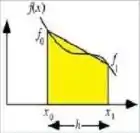
Se considerarmos a integral definida , o valor encontrado para utilizando a regra dos trapézios será equivalente a:

1. Área do trapézio
2. Média aritmética entre as áreas sobre a curva e a do trapézio
3. Diferença entre a área do trapézio e a área sobre a curva
4. Área sobre a curva
5. Soma entre a área do trapézio e a área sobre a curva

Fala Aíí!! Vamos relembrar um pouquinho de integral??

Por definição Integral é a área sob a curva, beleza?! Na regra dos trapézios nó vamos nos concentrar na área do Trapézio pra solucionar a integral...

Lembra da fórmula para calcular a Área de um Trapézio?

Diz aí, fórmula da área do trapézio não é beeeeem parecida com a Integral?

No nosso caso a altura () é a distância no intervalo [a,b] no eixo x em que a função está inserida e também o nosso passo já visto anteriormente, o trapézio menor é o e o trapézio maior é o , sacou?!

Logo, a nossa resposta é a letra A!!