Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra dos Trapézios

Exercício 41235678910

Enunciado

Empregando-se a Regra dos Trapézios para calcular a integral de x 3 entre 0 e   1 , tem-se como resposta o valor de:

  1. 0 . 3
  2. 0 . 5
  3. 0 . 4
  4. 0 . 2
  5. 0 . 6

Passo 1

Fala Aíí!! Nesse exercício queremos utilizar a regra trapézio para calcular a integral abaixo

∫ 0 1 x 3 d x

Beleza?! Como podemos fazer isso?? Temos que o gráfico da função x 3 no intervalo entre 0 e 1 é:

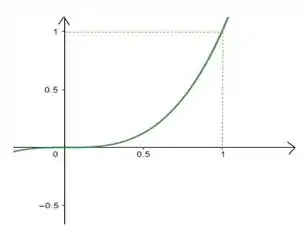
Precisamos utilizar a fórmula da área do trapézio para calcular a integral!

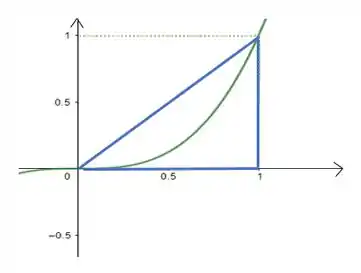
Lembrando que estaremos lidando com um erro.

Passo 2

A fórmula da área do trapézio é dada por:

A T = B + b h 2

Beleza?! Assim, temos que a base maior será

B = f 1 = 1

E a base menor será

b = f 0 = 0

Certo?! E a altura h ?

A altura h é dada pela diferença entre os limites de integração:

h = 1 - 0 = 1

Assim, substituindo os valores na fórmula, temos

A T = 1 + 0 1 2 = 0.5

Beleza?!

Logo, a nossa resposta é a letra B!

Resposta

Letra B!