(Adaptada) Uma placa fina de aço (, e ) está inicialmente a e é resfriada por um jato de água colidindo em uma de suas superfícies. A temperatura da água é de e o jato mantém um coeficiente de convecção na superfície elevado e aproximadamente uniforme. Considerando que a superfície é mantida à temperatura da água através do resfriamento, quanto tempo levará para a temperatura alcançar a uma distância de da superfície?
Dica: Assuma que a derivada da função em relação ao coeficiente de convecção () é sempre maior que a derivada da função .
Passo 1
A gente pode ilustrar o enunciado da seguinte maneira:
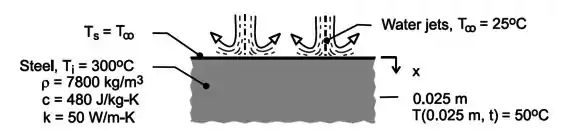
Esse caso trata de convecção numa superfície, logo estamos falando do Caso 3. A gente já viu que existe uma expressão pronta para a razão entre temperaturas:
No enunciado tá escrito que “o jato mantém um coeficiente de convecção na superfície elevado”. Ou seja, seu valor é muito alto! Podemos então analisar a equação quando o tende ao infinito ()!
Note que o primeiro termo não depende de , mas o segundo sim! Então bora analisar primeiro a exponencial e depois a função !
Passo 2
Analisando o termo exponencial:
Analisando o termo gaussiano:
Sendo assim, a gente pode verificar pela regra de L’Hospital a razão:
O limite quando dá a indeterminação e, então, a gente pode derivar em cima e em baixo:
Aí é que vem a dica! Como a derivada da função exponencial em relação ao coeficiente é sempre menor que a derivada da função , a razão vai a zero quando . Dessa forma, a gente fica com:
Passo 3
Como a gente já sabe a temperatura inicial () e final () e a temperatura do fluido (), bora calcular o valor da razão:
Passo 4
Então, temos que:
Pela tabela, temos que o argumento da função erro complementar será aproximadamente:
Isolando o termo do tempo:
Bora, então, calcular a difusividade térmica () do material:
Substituindo os valores do enunciado: