A massa específica e o calor específico de um material plástico são conhecidos ( e ), mas sua condutividade térmica é desconhecida. Para determinar a condutividade térmica, uma experiência é realizada, na qual uma amostra fina de um material é aquecida a uma temperatura uniforme de e então resfriada pela passagem de ar a sobre uma superfície. Um termopar fixado a uma distância de abaixo da superfície registra a resposta térmica do plástico durante o resfriamento.
Se o coeficiente de convecção associado com a corrente de ar é e a temperatura é registrada após iniciar o resfriamento, qual é a condutividade térmica do material?
Passo 1
A gente pode ilustrar o enunciado da seguinte maneira:
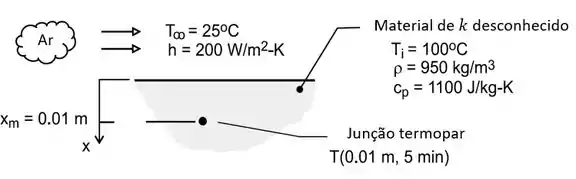
Esse caso trata de convecção numa superfície, logo estamos falando do Caso 3. A gente já viu que existe uma expressão pronta para a razão entre temperaturas:
Note que a condutividade térmica () só aparece dentro da definição de difusividade térmica () na expressão acima. Sendo assim, a gente precisa abrir a expressão de :
Mas é uma equação implícita! Ou a gente resolve por um método numérico (como Newton-Raphson ou Bisseção), ou a gente resolve com uma calculadora científica! Mais fácil pegar uma HP então!
Passo 2
Como a gente já sabe a temperatura inicial () e final () e a temperatura do fluido (), bora calcular o valor da razão:
Passo 3
Então, temos que:
Substituindo os seguintes valores do enunciado para resolver na HP:
Sendo assim, a gente fica com: