Um ferro para soltar cerâmica consiste em uma placa maciça mantida a por um aquecedor elétrico incorporado. O ferro é colocado em contato com uma cerâmica para promover o amolecimento do adesivo, permitindo que a cerâmica seja levantada facilmente da base na qual ela se encontra fixada. O adesivo irá amolecer suficientemente se aquecido acima de por um tempo mínimo de , mas sua temperatura não deve exceder para evitar deterioração do adesivo.
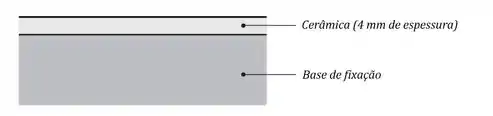
Considere a cerâmica e a base de fixação com temperatura inicial de e propriedades termofísicas equivalentes a: e .
Quanto tempo levará um trabalhador usando tal dispositivo para suspender a cerâmica?
A temperatura do adesivo irá exceder ?
Se o dispositivo tem área superficial quadrada de de lado, qual a quantidade de energia é removida do mesmo durante o tempo que leva para suspender a cerâmica?
Passo 1
Quanto tempo levará um trabalhador usando tal dispositivo para suspender a cerâmica?
Esse caso trata de uma superfície com temperatura constante, logo estamos falando do Caso 1.
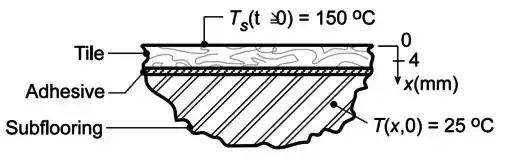
A gente já viu que existe uma expressão pronta para a razão entre as temperaturas nessa condição, que é dada por:
Bora então calcular a difusividade térmica () do material:
Sendo assim, considerando que a superfície tem que atingir , temos que:
Pela tabela o argumento da função erro que gera aproximadamente o resultado vale 0,92. Então:
Passo 2
A temperatura do adesivo irá exceder ?
Depois que a temperatura alcançar os , ela deve permanecer por, no mínimo . Então, a gente tem que avaliar qual a temperatura da superfície depois do tempo total :
Utilizando novamente a equação para o Caso 1, mas agora usando o tempo pra calcular a temperatura, teremos:
Pela tabela:
Isso equivale a , ou seja, a temperatura não ultrapassa o limite de após o tempo total.
Passo 3
Se o dispositivo tem área superficial quadrada de de lado, qual a quantidade de energia é removida do mesmo durante o tempo que leva para suspender a cerâmica?
O fluxo de energia térmica nessa condição do Caso 1 é dado pela seguinte equação:
Esse fluxo varia ao longo do tempo, como vemos na equação. Então, pra gente encontrar a quantidade total de energia que será transferida do asfalto, basta a gente integrar essa expressão ao longo do tempo:
Substituindo a expressão do fluxo:
Integrando a expressão:
Já calculamos o valor da difusividade térmica (), então: