Padrões para paredes contrafogo podem ser baseados em suas respostas térmicas a um fluxo térmico radiante especificado. Seja uma parede de concreto com de espessura (, e ), que se encontra a uma temperatura inicial de e é irradiada em uma superfície por lâmpadas que fornecem um fluxo térmico uniforme de . A absortividade da superfície em relação à radiação é . Se as exigências de construção ditam que as temperaturas nas superfícies irradiada e não-irradiada, após de aquecimento, não podem exceder e , respectivamente, as exigências serão atendidas?
Passo 1
A gente pode entender o enunciado com a seguinte ilustração:
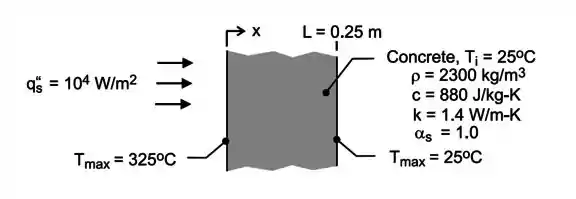
Nessa situação, temos um fluxo de calor constante na superfície de valor conhecido (). Sendo assim, a gente está no Caso 2 e temos uma expressão pronta para determinar a temperatura em algum ponto do material:
Passo 2
Bora, primeiro, calcular a difusividade térmica () do material:
A gente precisa calcular a temperatura das duas superfícies após : em e em . Mas antes bora calcular o termo que é constante nas duas situações:
Vamos agora determinar a temperatura em cada superfície após 30 minutos.
Passo 3
- No instante de em :
- No instante de em :
Assim:
Como é menor que o limite de , a condição ainda é satisfeita após para a parede na posição .
Passo 4
Substituindo os demais valores:
Assim:
Pela tabela:
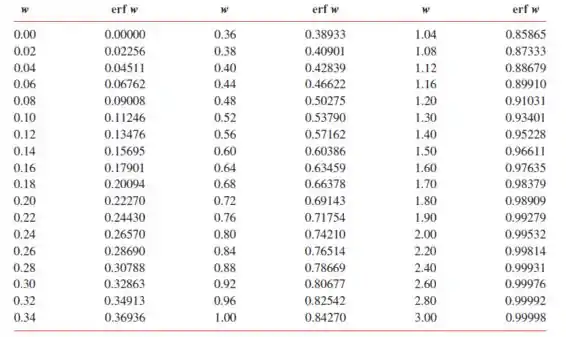
Podemos ainda escrevero como sendo :
Assim, ficamos com:
Como é menor que o limite de , a condição ainda é satisfeita após para a parede na posição .
Resposta
Ambas as condições são satisfeitas, porque as temperaturas nas superfícies, após são de: