Calcule a integral indefinida

Vamos lá. Vamos direto ao ponto...

Temos a seguinte integral para resolver

Mas agora temos um problema... Como resolver essa parada?

Resolvendo pelo método da substituição simples, vamos pegar a parte que parece ser mais complicada, no caso, o que pode enrolar a gente ali, e vamos fazer as seguintes substituições...

Agora vamos derivar esse :

Repara que aparece na derivada, justamente um pedaço da nossa integral.

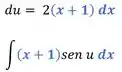
Vamos só trocar de lugar o com o , que isso vai ficar mais claro:

Para substituir o precisamos deixar ele sozinho em . Então vamos jogar o que está multiplicando, para o outro lado dividindo:

Agora é só substituir na integral:

Então nossa integral fica assim, ó:

Agora fica muito mais fácil integrar.

Colocamos a constante para fora

E lembramos que a integral do seno é menos cosseno, então nossa integral será:

Agora é só “Re-substituir” o valor de pra voltarmos pra variável . Lembrando que , vamos ter o seguinte: