Calcule a integral

Vamos lá pra mais uma resolução... Temos a seguinte integral para resolver

Beleza, mas como resolver essa parada?

Precisamos transformar nossa integral complicada, em uma integral mais simples. Resolvendo pelo método da substituição simples, podemos reescrever esse integral de , em uma nova variável que fará ela ficar mais tranquila de resolver. Pra isso vamos fazer as seguintes substituições...

Encaixando isso na integral:

Ela se torna:

Mas ainda temos o e o na integral, então vamos atrás de substituir eles também. Pra isso vamos derivar o , e teremos:

Vamos passar o para o outro lado:

Repare que quando fizemos isso, encontramos um outro pedaço que também está na nossa integral:

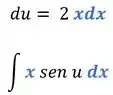
Vamos trocar o de lugar com o , pra isso ficar mais claro:

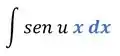
Para substituir o precisamos deixar ele sozinho na derivada de . Então vamos jogar o que está multiplicando, para o outro lado dividindo:

Então nossa integral fica assim ó

Prontinho, ela está toda escrita em função de Agora vamos resolver. Colocamos a constante para fora

E lembramos que a integral do seno é igual a menos cosseno:

Resolvido. Mas temos que “Re-substituir” o valor de porque a pergunta era em e não em , e vamos ter o seguinte

Agora sim! Tudo pronto. Mas uma resolvida!