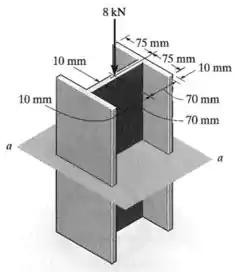
A coluna está sujeita a uma força axial de aplicada no centroide da área da seção transversal. Determine a tensão normal média que age na seção . Mostre como fica essa distribuição de tensão sobre a seção transversal da área.
Passo 1
A tensão normal média , pedida pelo exercício, é dada pela divisão da força normal interna (que é igual à força aplicada de ) e a área da seção transversal da coluna.
Para calcular a área , devemos observar sua geometria:
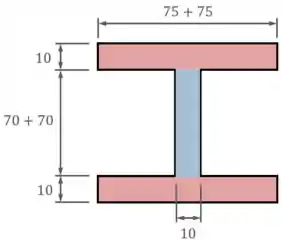
Da imagem, vemos que a área é composta por duas áreas “vermelhas” de largura e comprimento , e uma área “azul” de largura e comprimento .
Sendo assim:
Usando a fórmula da tensão normal média:
Como :
Resposta
A distribuição de tensão sobre a seção transversal é uniforme:
Exercícios de Livros Relacionados
Cada uma das barras da treliça tem área de seção transversal de 780 m m ² ². Se a tensão normal média máxima em qualquer barra não pode ultrapassar 140M P a , determine o valor máximo P das cargas que
O quadro mostrado consiste em quatro elementos de madeira, ABC, DEF, BE e CF. Sabendo que cada elemento tem seção transversal retangular de 2 x 4-in e que cada pino tem um diâmetro de 1/2 in., determi
Três forças, cada uma de intensidade P= 4 kN, são aplicadas a estrutura mostrada. Determine a área da seção transversal da parte uniforme da haste BE para a qual a tensão normal é de +100 MPa.
Uma carga axial de 40 kN é aplicada a uma coluna curta de madeira, suportada por uma base de concreto apoiada em solo estável. Determine (a) a tensão de contato máxima na base de concreto, (b) o taman
Para P = 100k N , determine a espessura t mínima necessária para a placa se a tensão admissível for de 125M P a .